Sensitivities: finding problems and setting priorities

Risk management must be efficient and is forced to make effective decisions with scarce resources. Finding the problematic risk drivers and being able to set justified priorities for management is therefore an important strategic goal of risk analysis.

Risk Kit and the Enterprise Risk Evaluator provide methods to assess sensitivities - the impact of risk factors on the bottom line. They answer a variety of possible guiding questions:

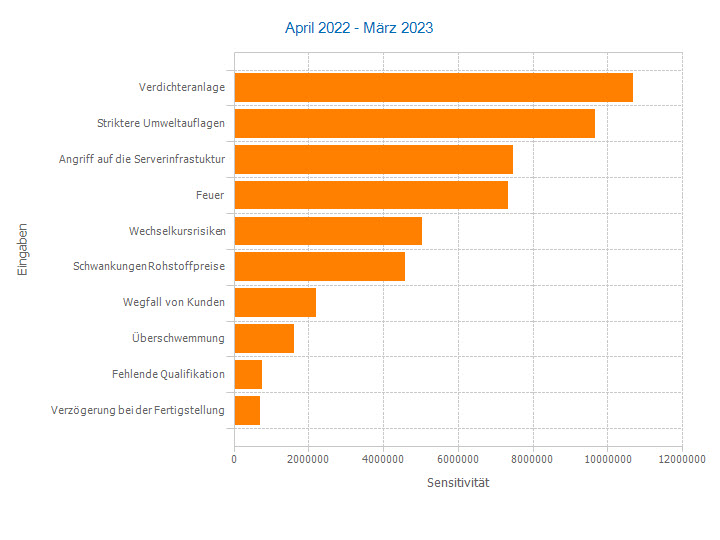
• Which risk factors have the greatest impact on the results? What are my top risks?
• What is the absolute impact of a risk factor on the outcome in the unit of outcome? 
• How do risk events affect the result when they occur?
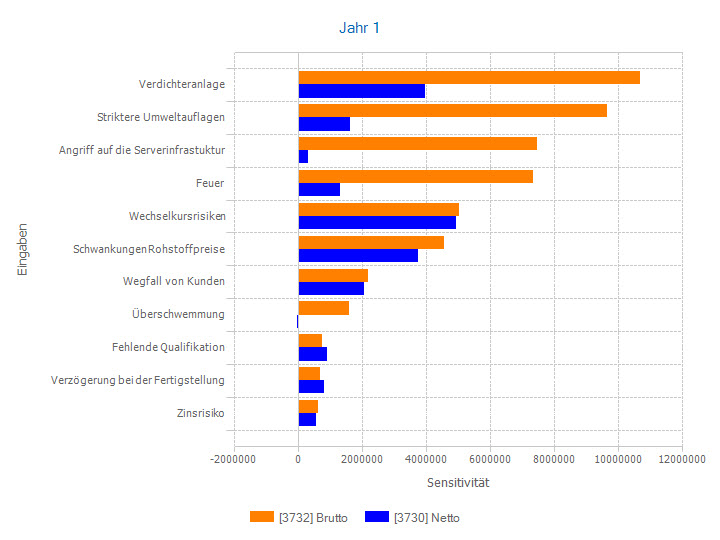
• Can I tell if a risk mitigating measure is ineffective?
• How do the individual risk factors contribute to the overall risk?
• How can I communicate the results in tabular and graphic form?

Here is an overview.

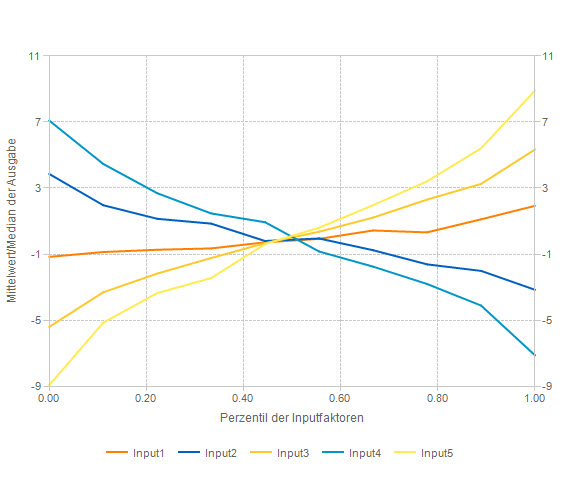
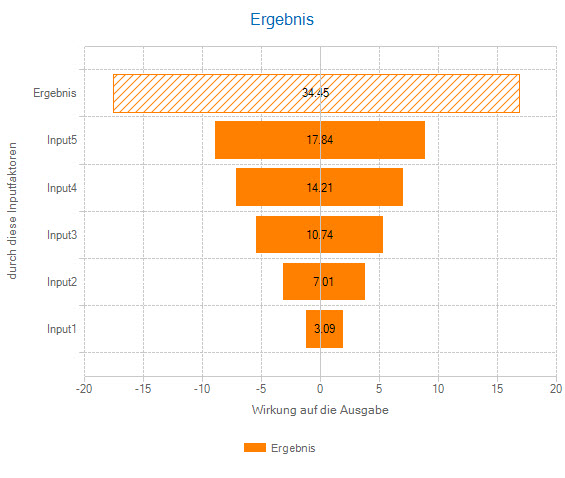
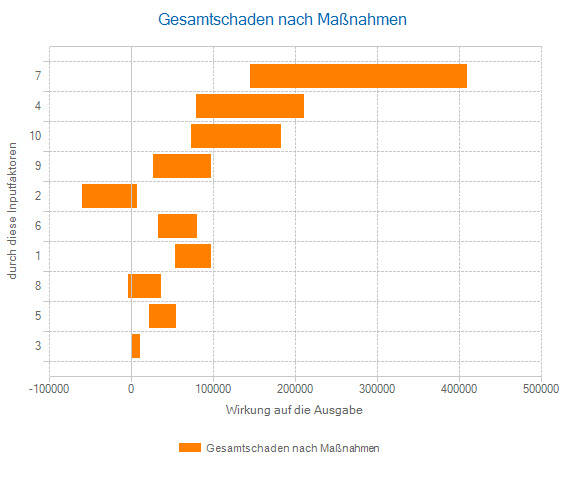
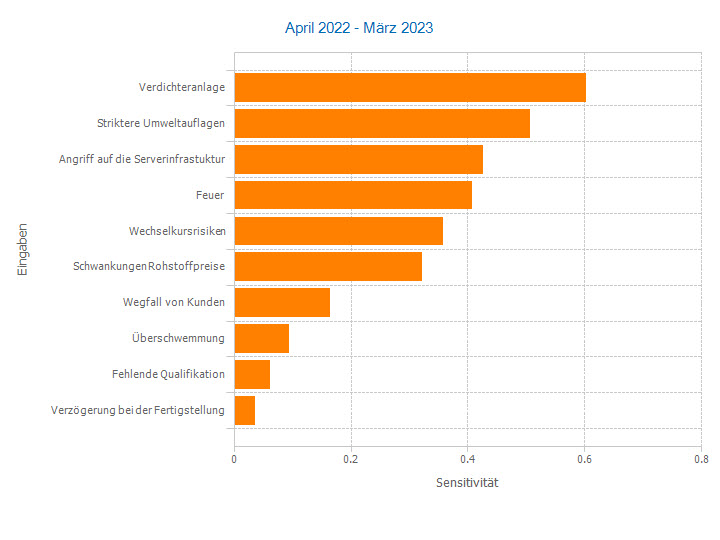
Absolute sensitivities capture the effect of a risk factor on the result in the unit of the result. All risk factors thus have a uniform 'currency' and are comparable with each other. They are calculated by taking the mean or median of the outcome for a quantile range of the risk factor (e.g. 0-10%, 10-20%, etc.).

The Spider Chart and the Tornado Chart illustrate these steps. They are a proven means of risk communication.

In enterprise risk management, this type of sensitivity is particularly interesting, because if a risk is not mitigated by measures, its effect on the result does not change under general circumstances. The sensitivity of this unmanaged risk then also remains stable. This is an important prerequisite for identifying measures that do not reduce the impact of the risk factor on the result.

For event-driven risk factors that do not always occur, but only sometimes, or that only take on a few values, there are conditional absolute sensitivities as a special type of sensitivity. Here, all outcomes for which the risk factor has the same value are condensed to one number by their mean or median. The absolute sensitivities are then calculated only on the different values of the risk factor.

The advantage of the conditional absolute sensitivities is that the case where the risk has not occurred at all or has a fixed value and therefore does not have a different effect is removed from the analysis. The focus is then on the question 'in which area does the result change if the risk factor changes?' Factors that certainly bring uncertainty into the system, but are also or even primarily opportunities and not risks, thus become visible.

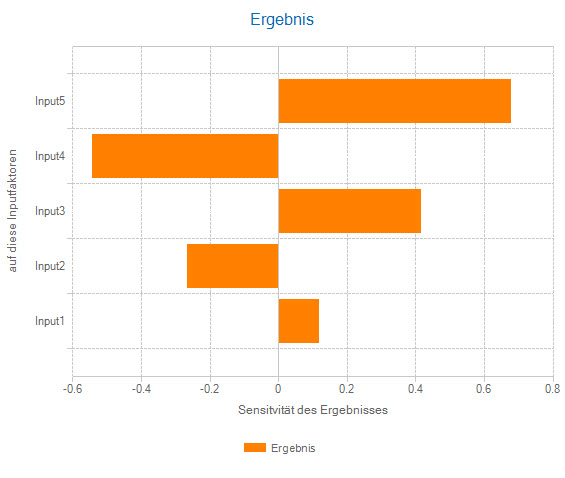
Relative sensitivity concepts put quantities in relation to each other. They therefore usually have no unit and move within a certain range of values.

Important relative sensitivities are linear correlations, rank correlations, contributions to variance (squared rank correlations whose sum is standardised to 1) and beta factors. Their magnitude indicates how closely risk factor and outcome are related. Their sign indicates the direction of the correlation.

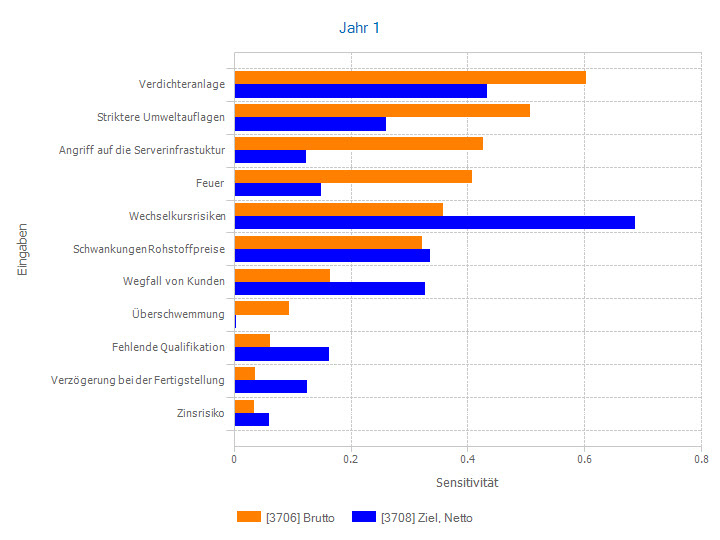
When measures are taken, this results in the peculiarity that relative sensitivities of risk factors for which there are no measures also change. As a rule, they become larger because their contribution to a smaller pie after measures, so to speak, now becomes larger in relative terms.

Correlations take values between -1 and 1. Contributions to variance cannot become negative. Their values lie between 0 and 1.

Beta factors are not limited in their range of values, but usually lie between -3 and 3. If their magnitude is greater than 1, this means that the covariance between the factor and the outcome is greater in magnitude than the variance of the outcome.

If the risk factor has a very high variance, caution is advised, as this can lead to the detection of a random spurious correlation. The use of the beta factor is thus particularly suitable if there is a known structural relationship between a risk factor and the result, e.g. between a share price and a share index in which the share itself is included.

Risks cause costs - also through risk management itself. In addition, there are capital costs for risk capital backing, which has recently been required in the risk-bearing capacity concept of IDW PS 340. Distributing the costs back to the risks is thus a natural application of the polluter pays principle.

In order to determine the risk contributions, you also specify the risk measure to be redistributed to the risks. This can be a value at risk (quantile) as well as an expected shortfall. The absolute sensitivities or beta factors are given the sign of the linear relationship between the risk factor and the result and are scaled so that they add up to this risk measure.