Expert and poly distributions

Applications in risk management must be able to do equal justice to expert assessments of an issue and data evaluations on a case-by-case basis.

Standard distributions, however, are usually restricted to a fixed form with little variation. Softening these restrictions and having more flexible and adaptable tools available has long been a goal of risk managers.

In Enterprise Risk Evaluator, Risk Kit and our other systems, there is therefore a spectrum of distributions with diverse forms and properties. New additions are now the expert and poly distributions. They can be limited or open at the edges, expand the freedom of experts and adapt to the particularities in the data.

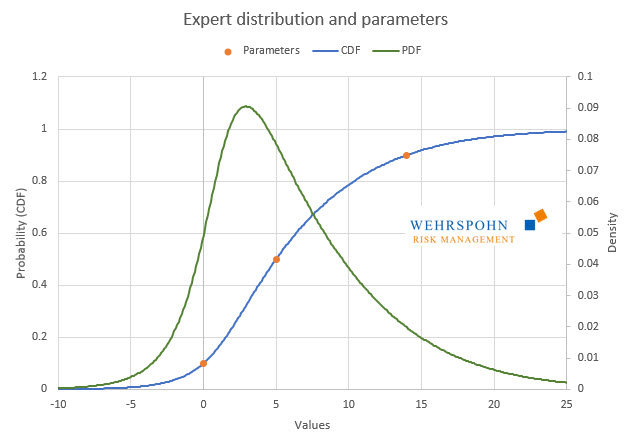
The expert distribution is a special case of the poly-distributions. It determines its shape via three quantiles and, if necessary, minimum and maximum, if the distribution is to be restricted. It is thus linked to the triangular and PERT distributions, but its shape is more flexible. For example, it also enables a one-sided or two-sided unlimited representation of effects. It can thus be used in areas where it is not possible to specify a maximum damage without further ado.

The quantiles used to determine the expert distribution are symmetrical about the median, i.e. they are the p-quantile, the median itself and the 1-p-quantile. In addition, lower and / or upper limits for the range of values can be specified if necessary.

The distribution passes exactly through the specified points.

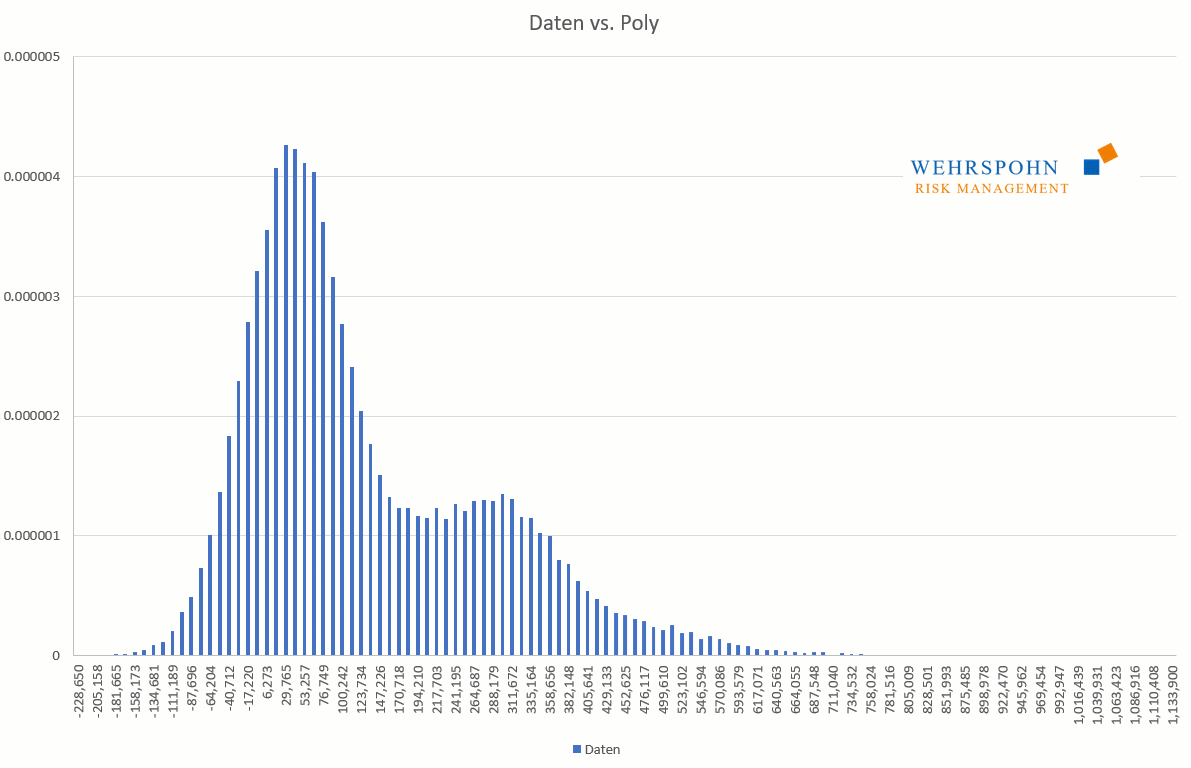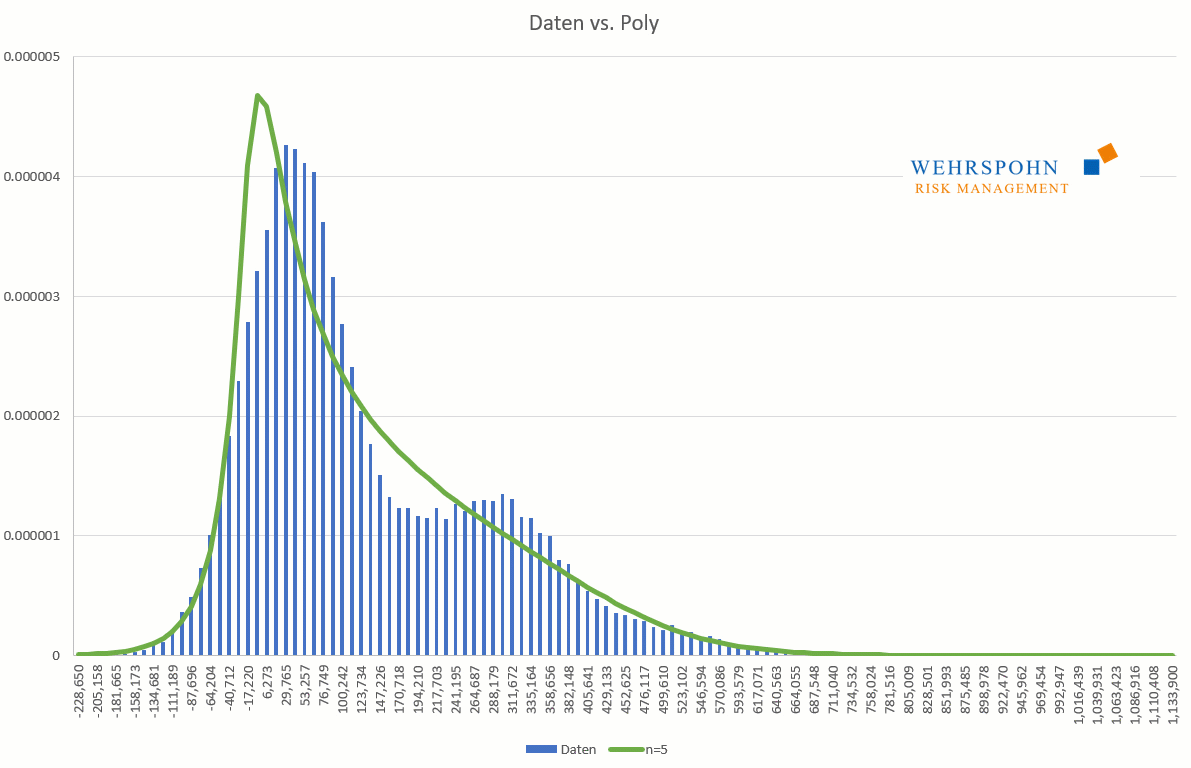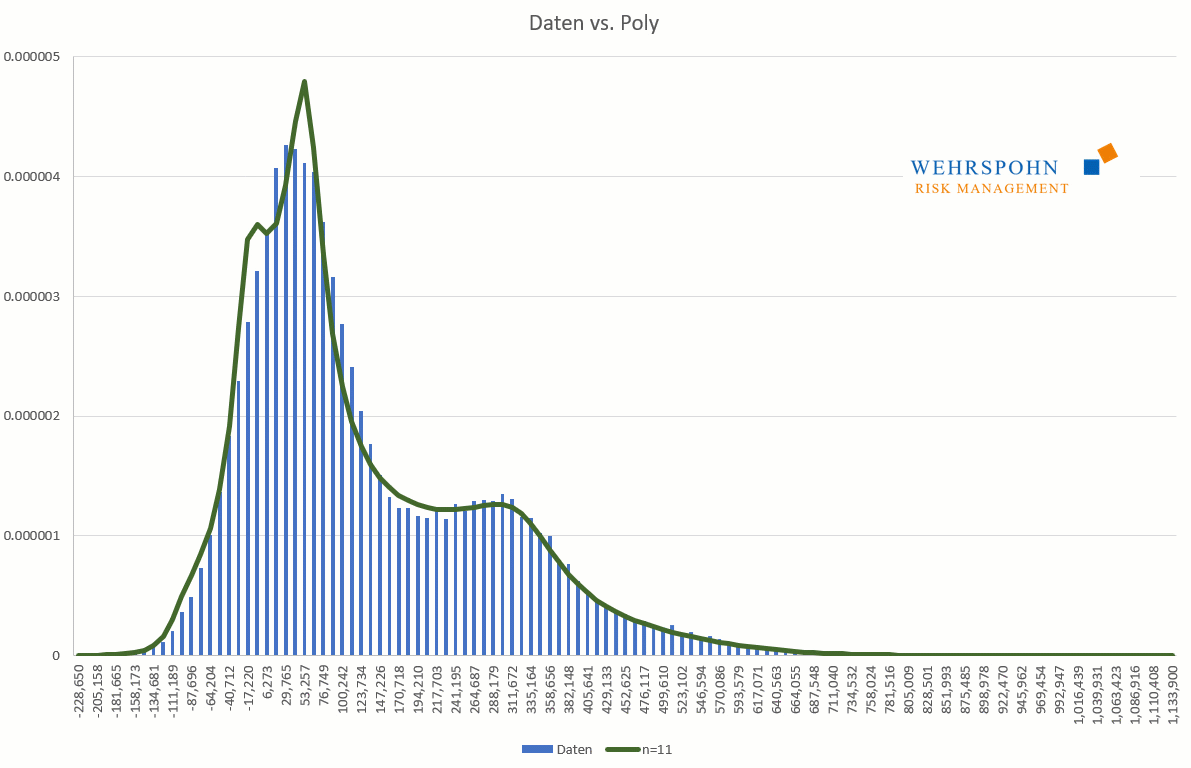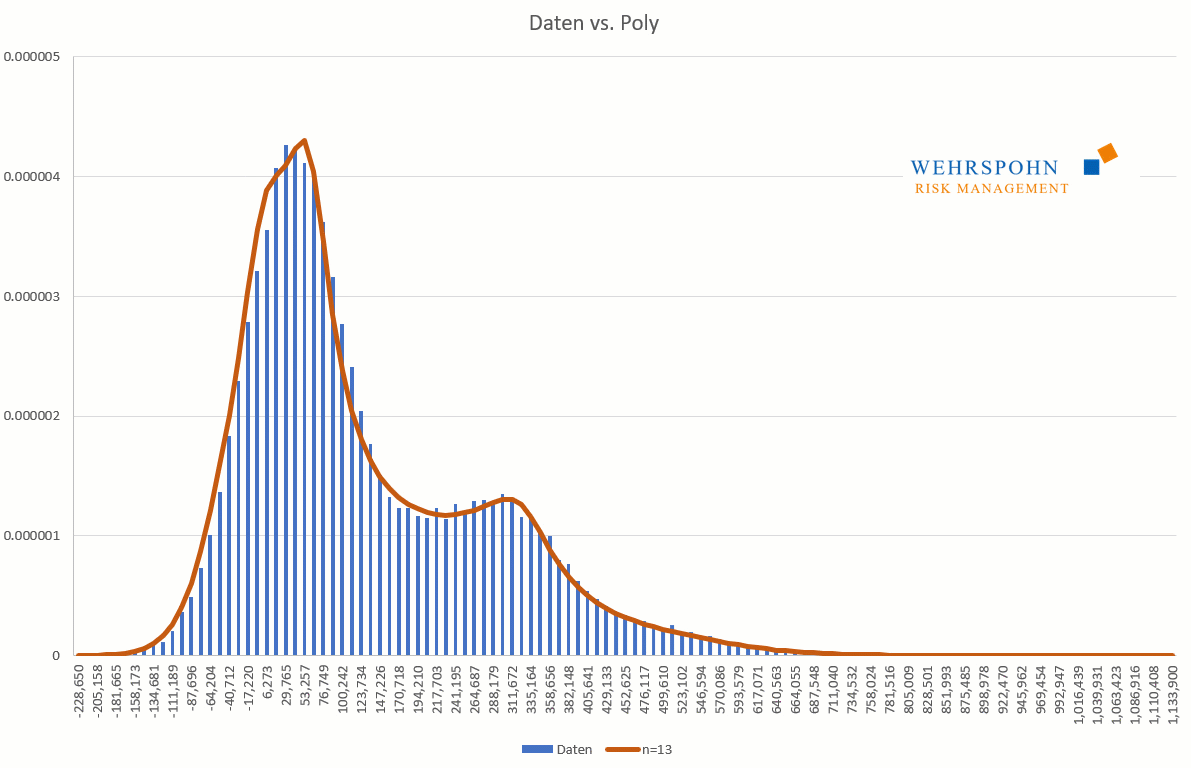
Poly distributions are a new[1] and very flexible tool in the description of risks. They gain their adaptability through their structure as a polynomial. Similar to how a Taylor series of a sufficiently high degree can approximate continuous and smooth functions with arbitrary precision, poly-distributions adapt to data or expert assessments in great detail.[2]

Poly distributions can take all forms at the boundaries. They can be unbounded on both sides (Poly), bounded on the left or right (PolyL or PolyR) or bounded on both sides (PolyLR).

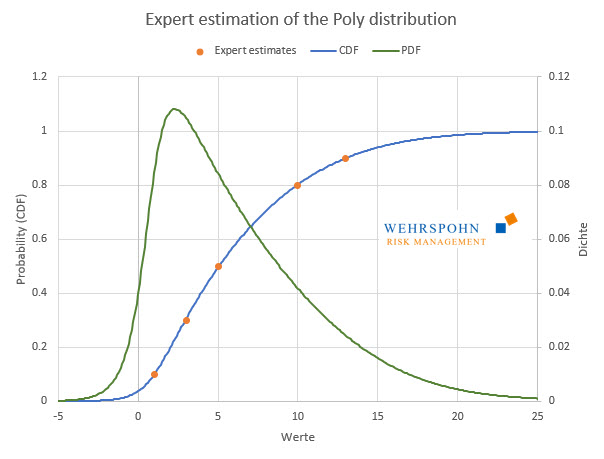
The coefficients of the polynomials are abstract and not accessible to experts. If the distributions are parameterised via expert estimates, this is therefore done via a list of quantiles, i.e. pairs of values and probabilities in the CalibratePoly function, which determines the polynomial coefficients from the quantiles.

Unlike the Expert distribution, a special case of the Poly distribution, the quantiles do not have to be symmetrical around the median, but can be freely chosen. The list must contain at least three and can contain any number of points. In addition, lower and upper limits can be specified if required. The distribution is selected so that it fits the data as seamlessly as possible. Boundaries are always hit exactly.[3]

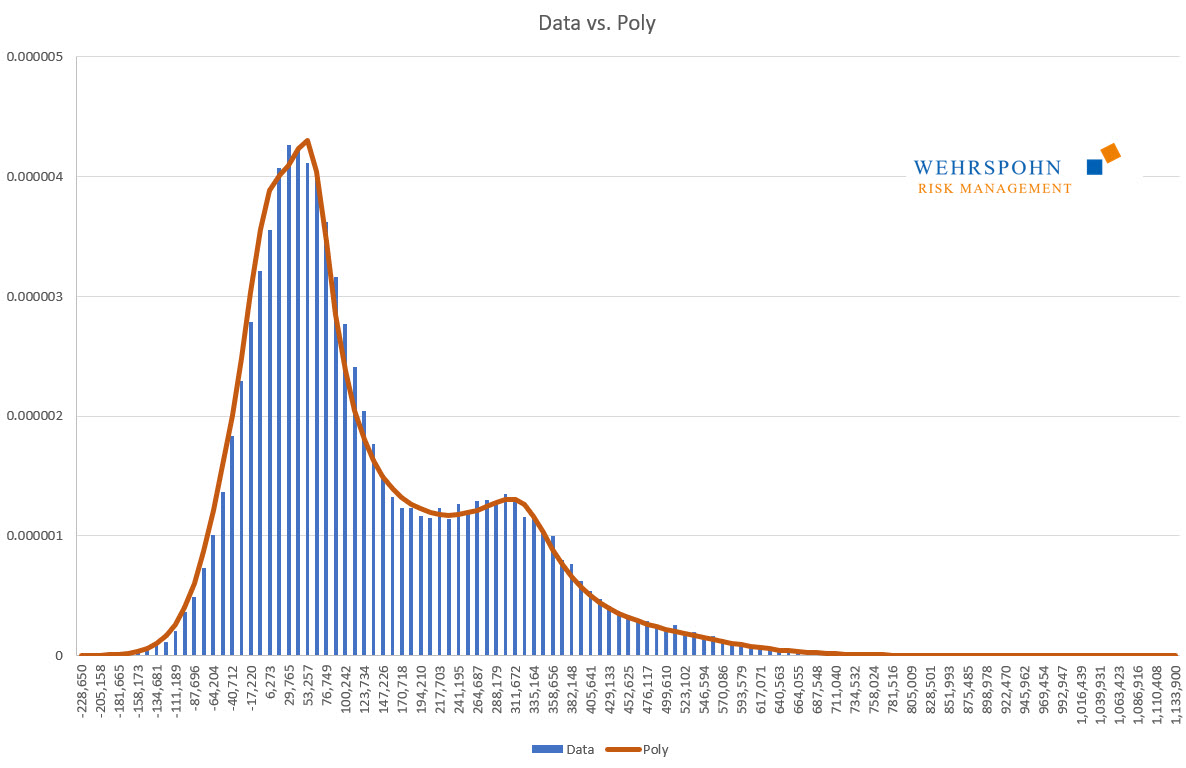
The second important application of poly-distributions is their fit to data. With observed data, this is a given. But simulated data also play an important role.

In ERM, all material risks of the company are to be considered together in one analysis. In many companies, however, there are special types of risk that are so important that they receive separate attention and systems specialised in this type of risk are used that perform simulations themselves. Typical examples are treasury applications or commodity purchasing.

With poly-distributions, the results of specialised simulations can be transferred to ERM very accurately with very little effort. This is also the case if the simulated distributions have a shape that cannot be mapped with standard distributions, e.g. if they have multiple modes. In simulated distributions, multiple modes arise naturally when large risks or crises occur in the simulation.

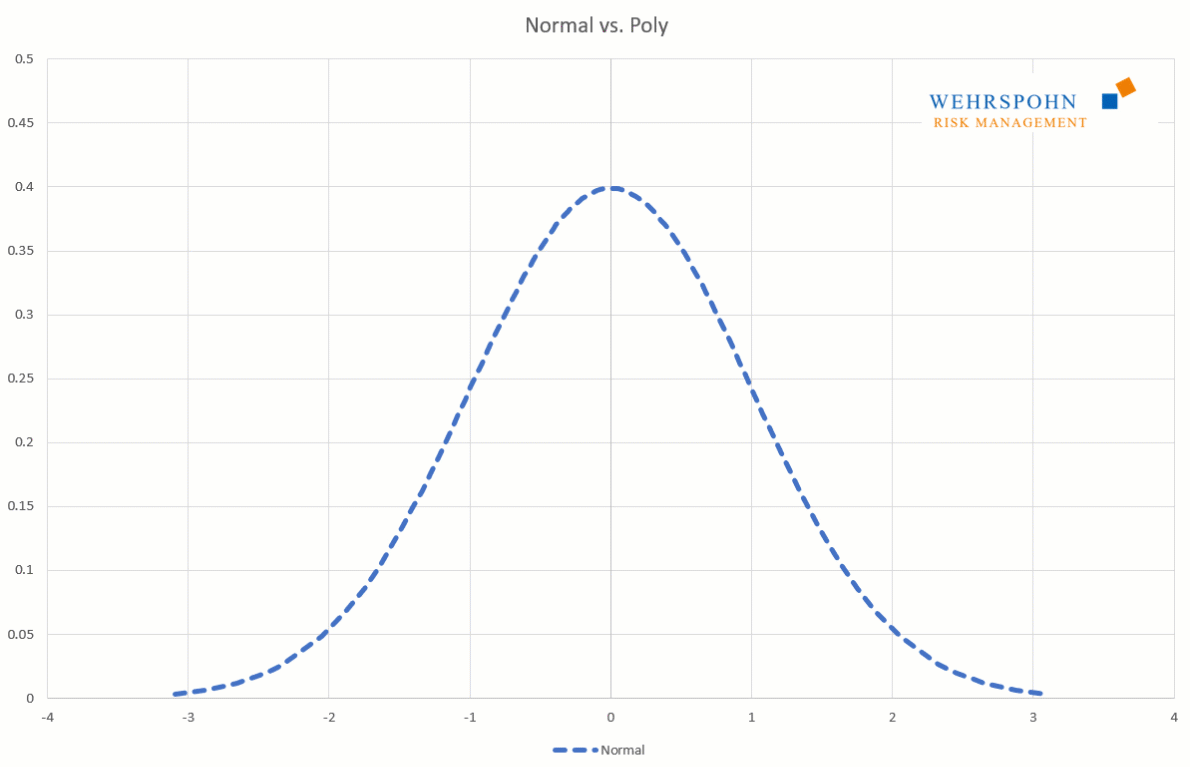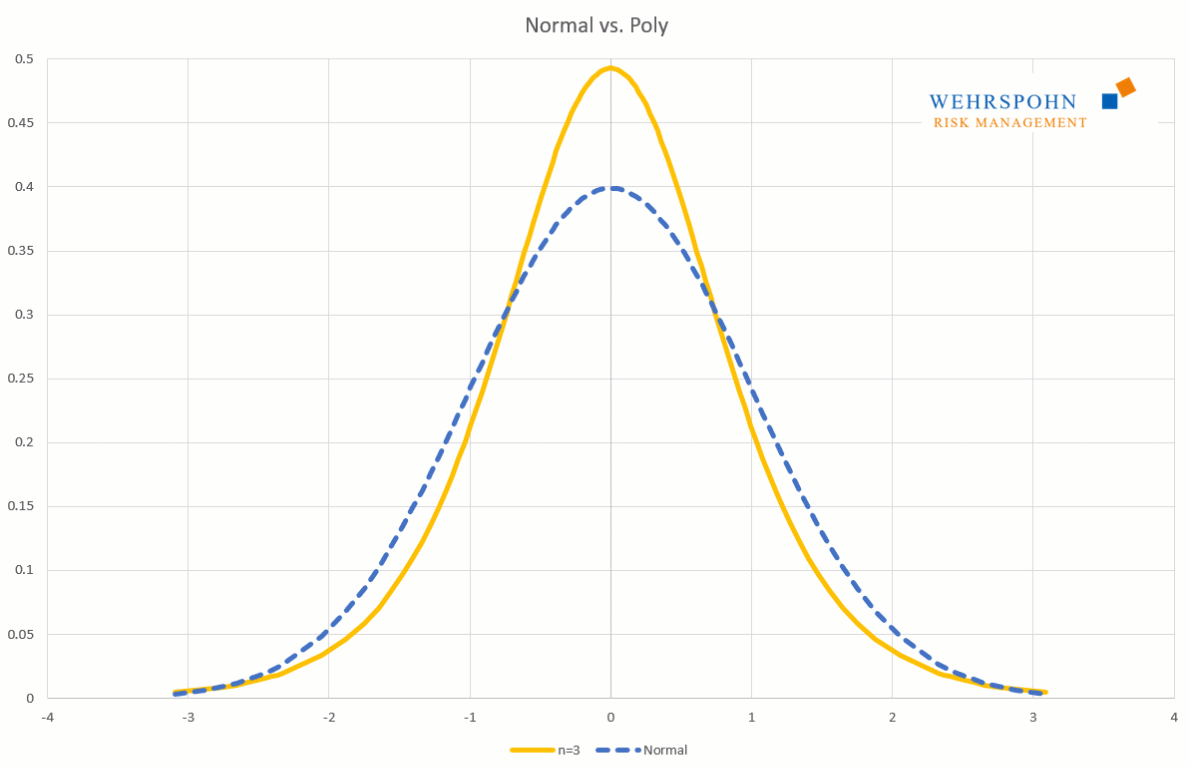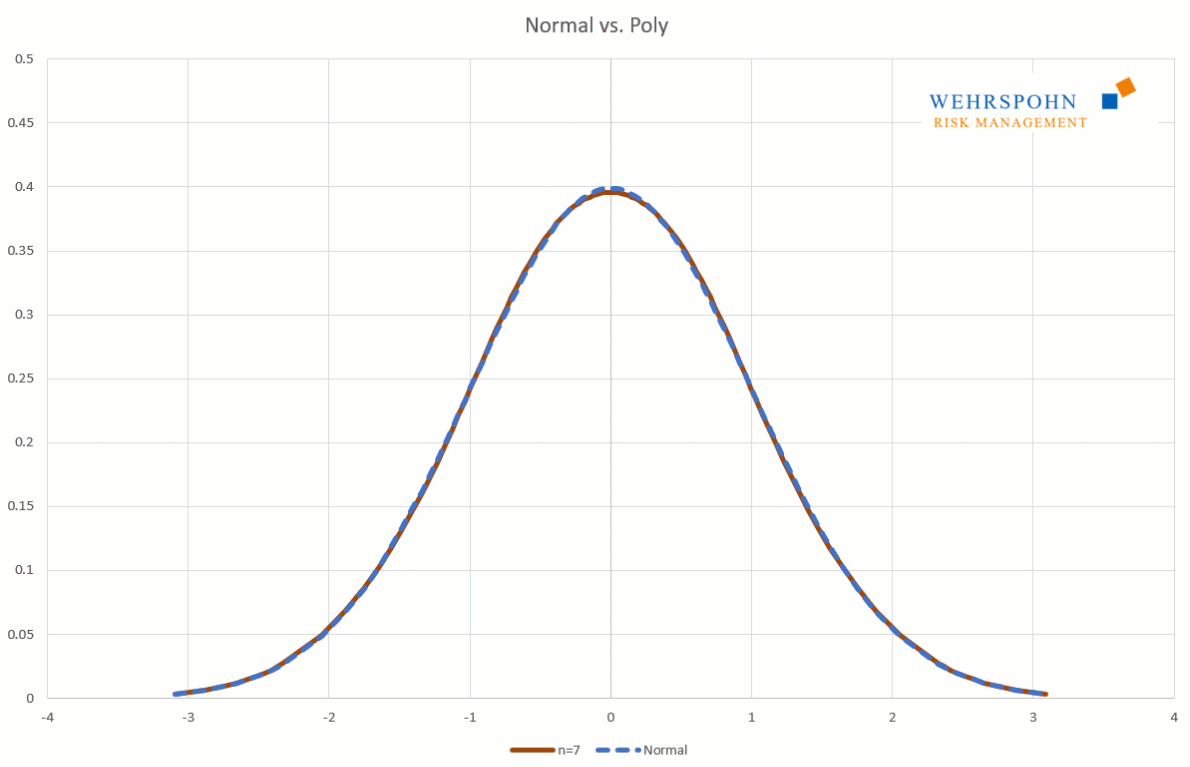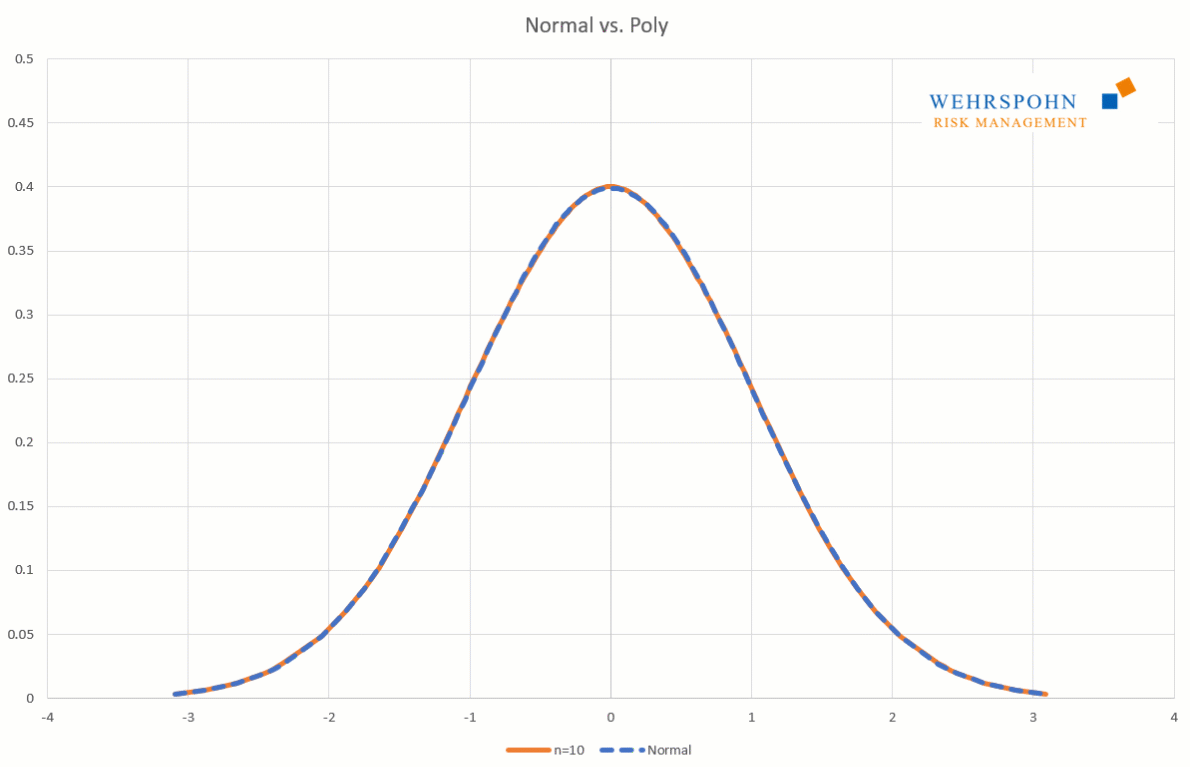
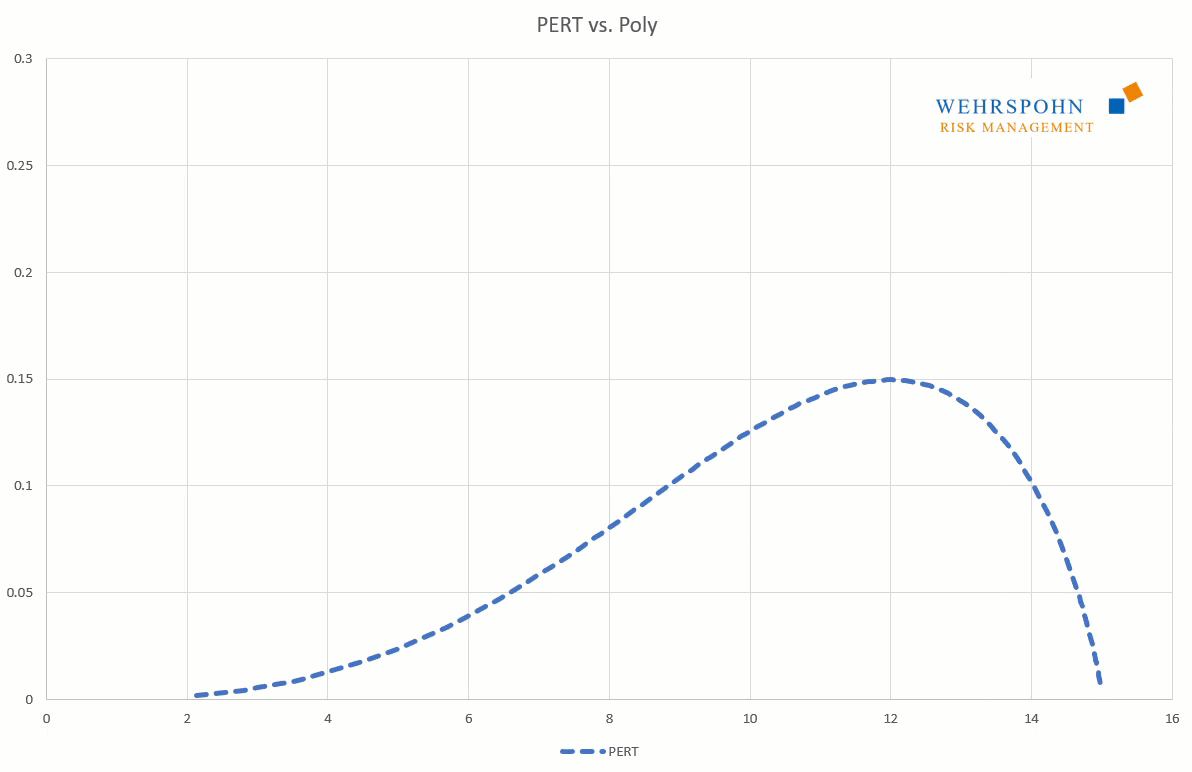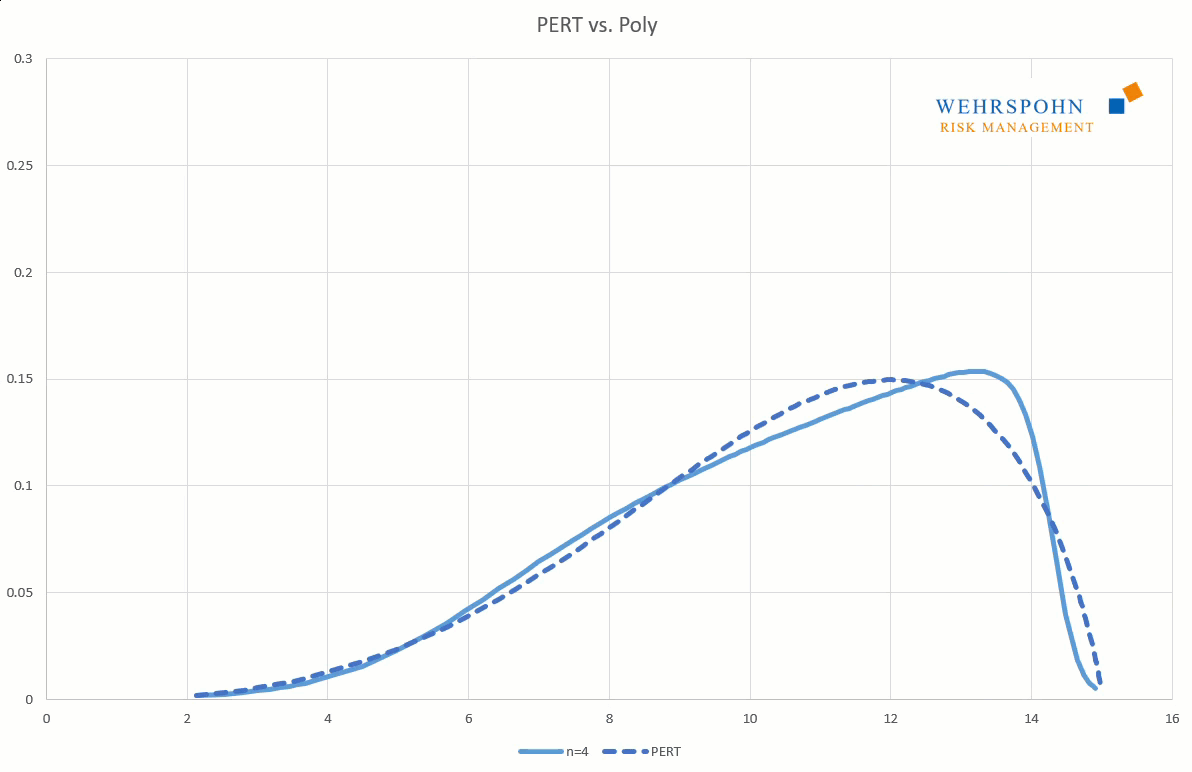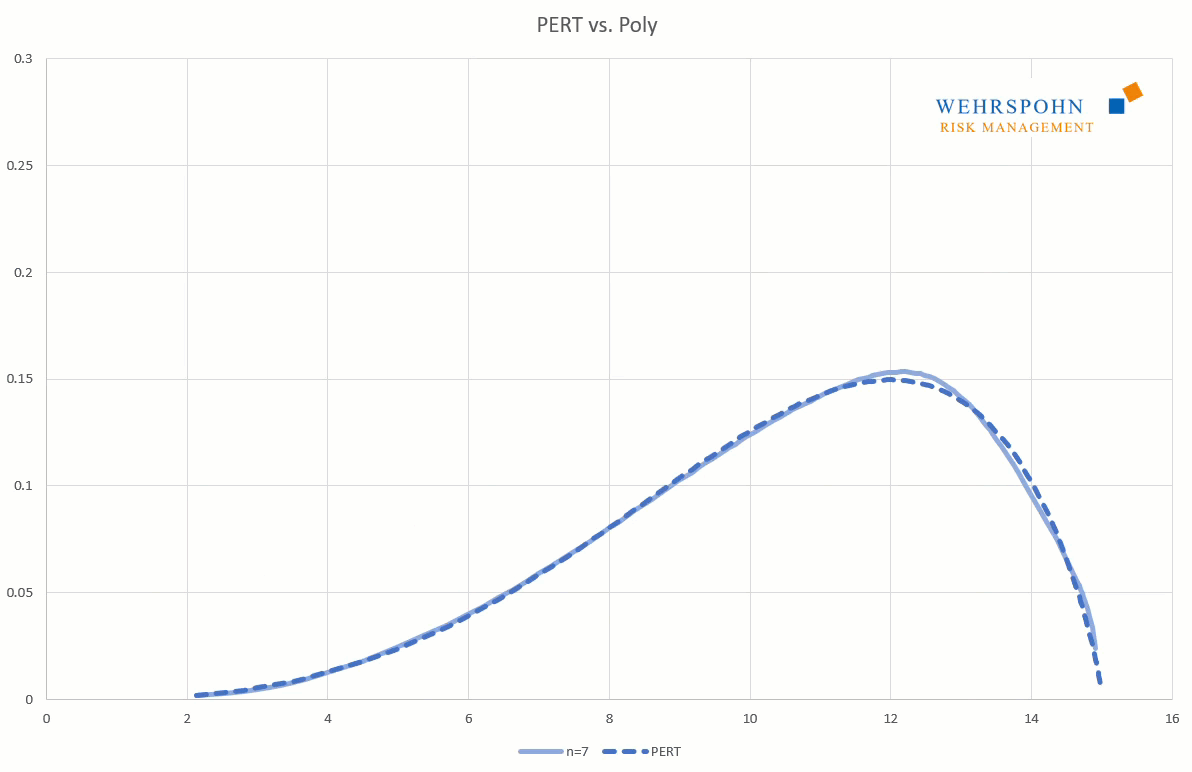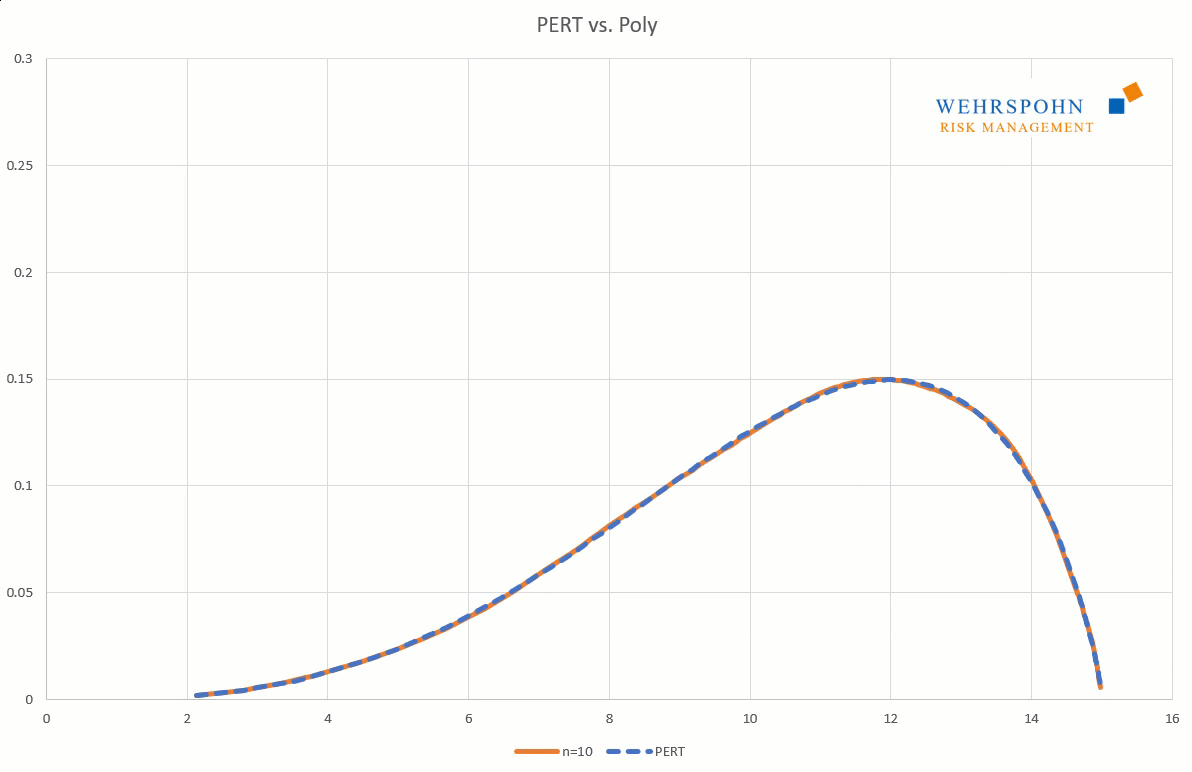
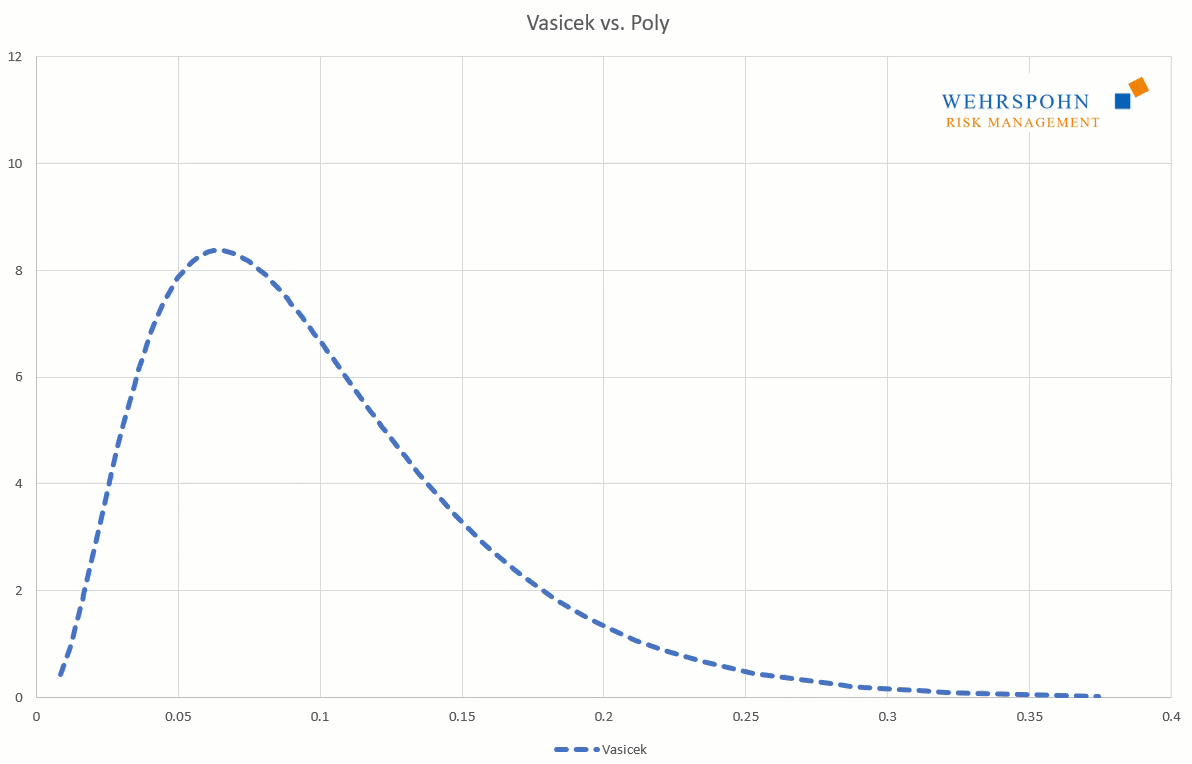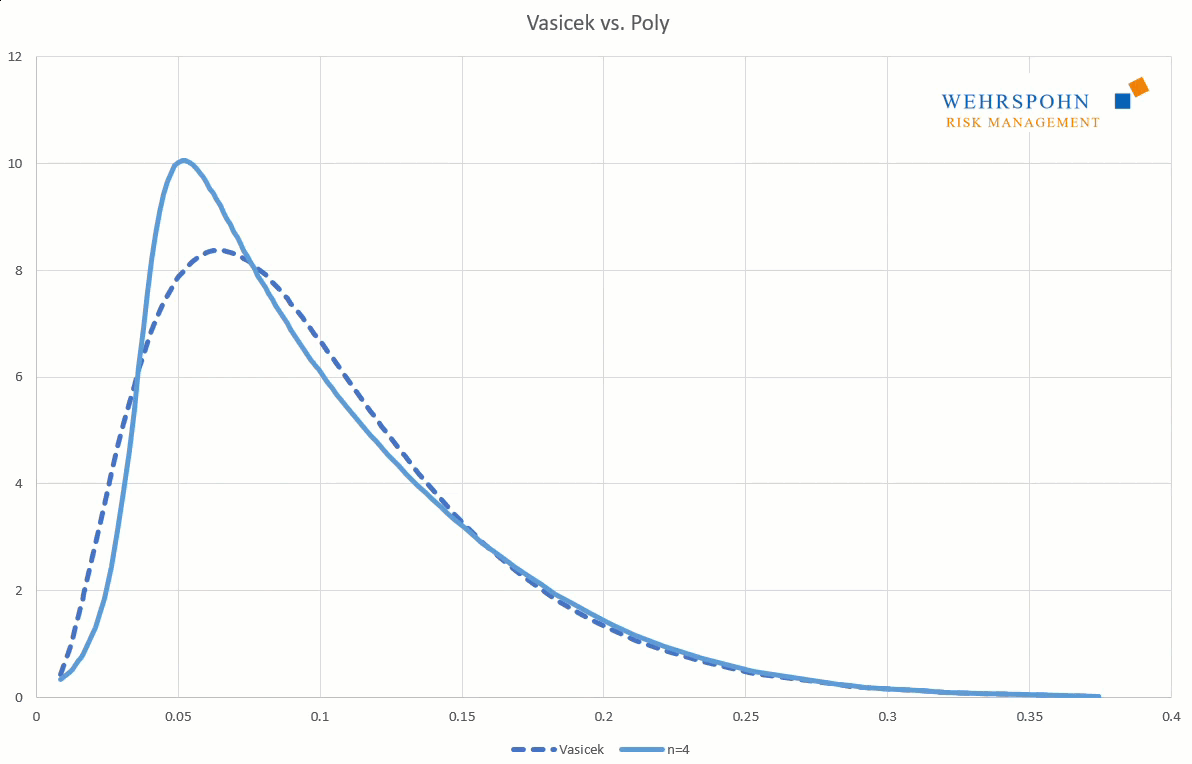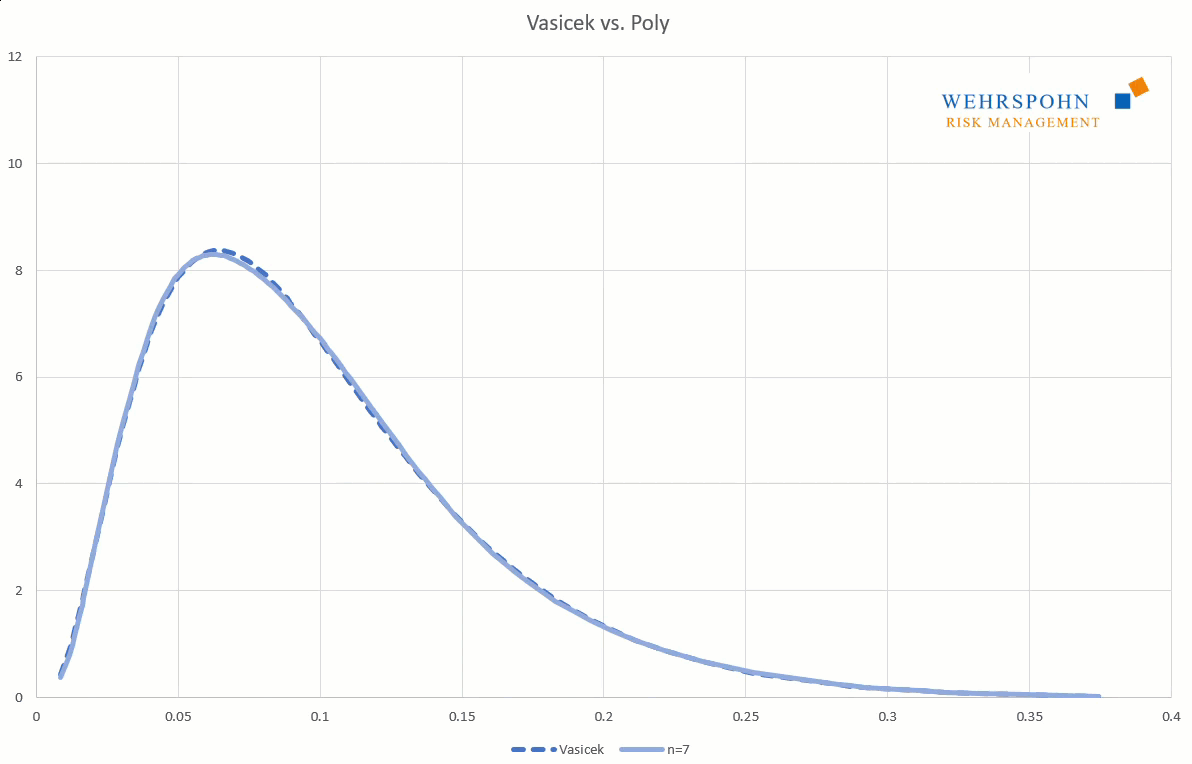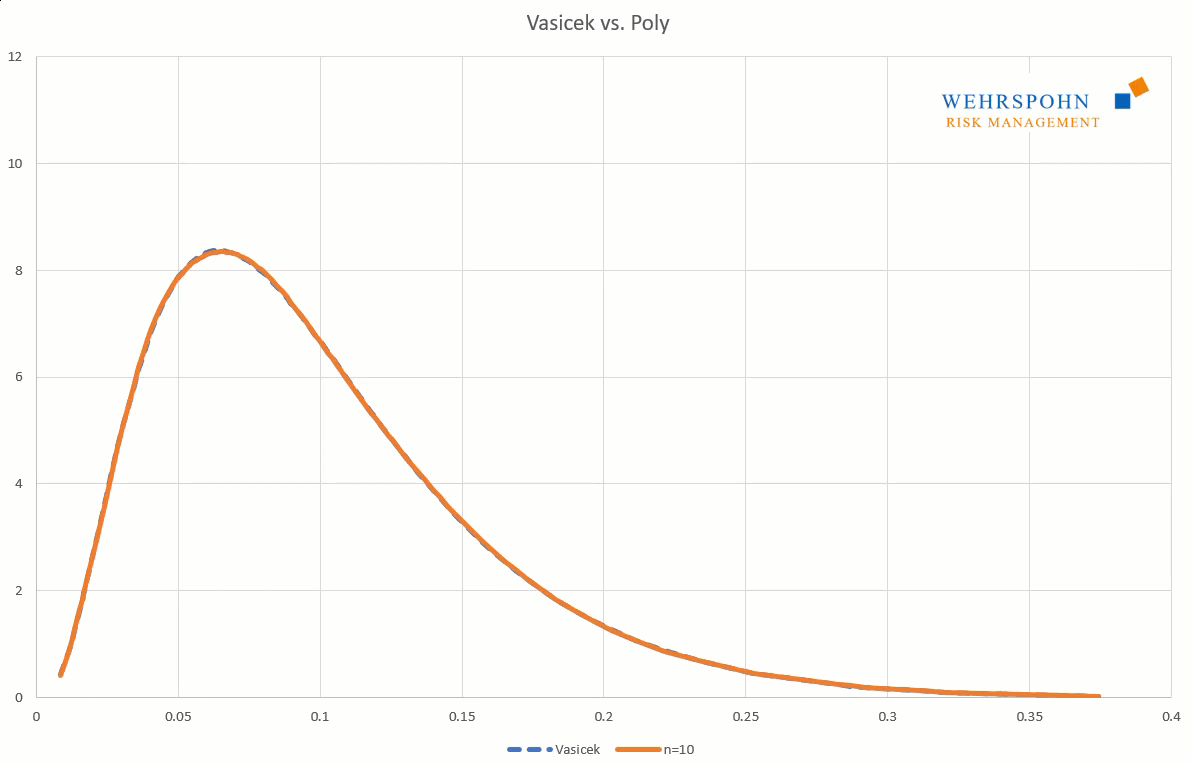
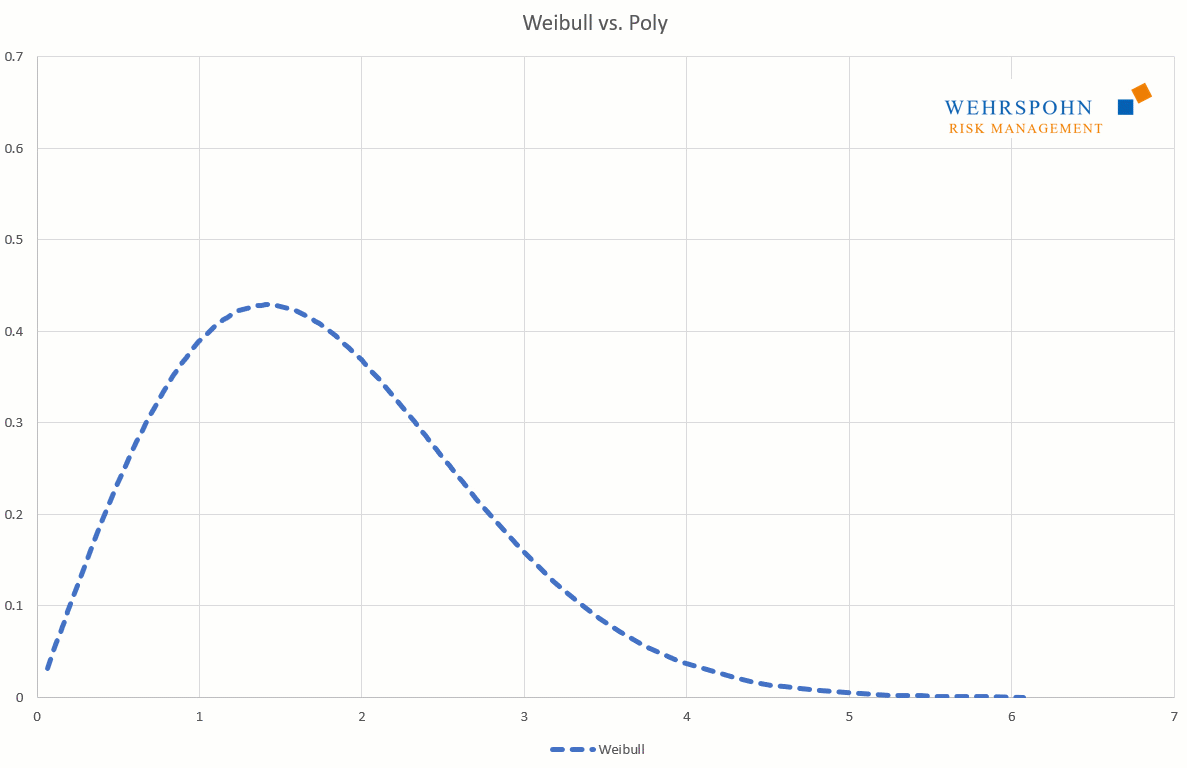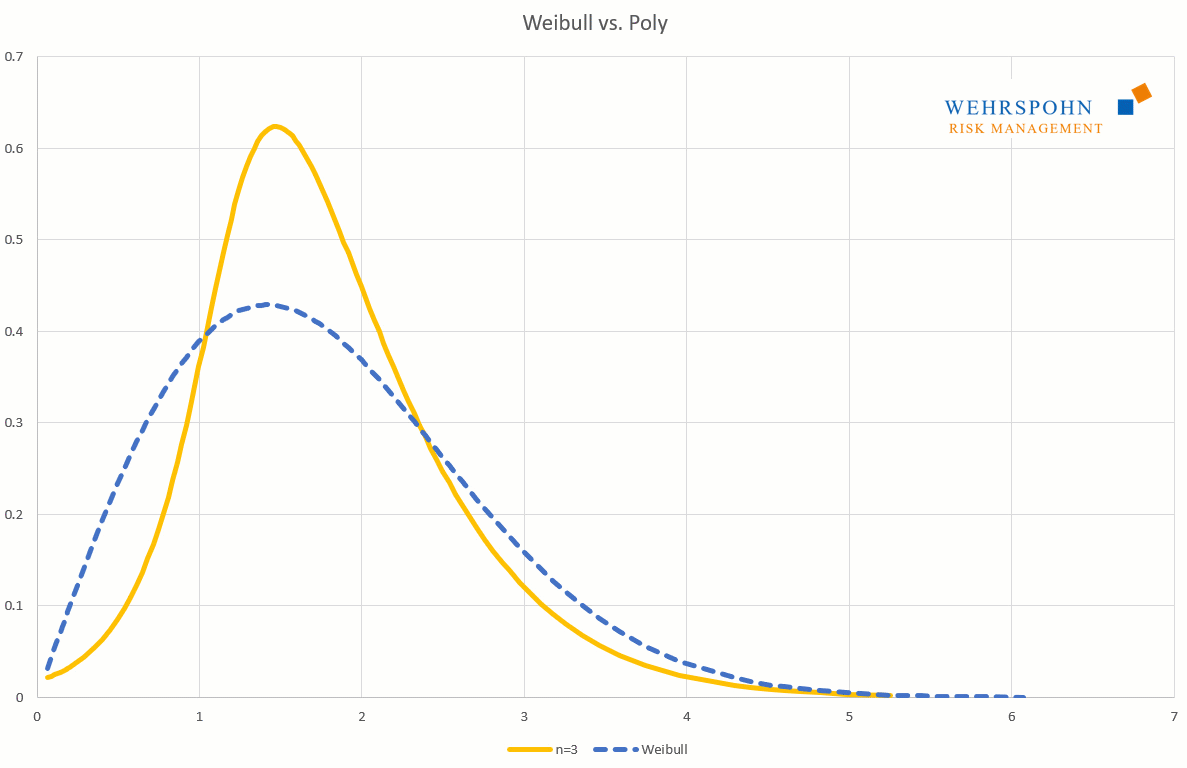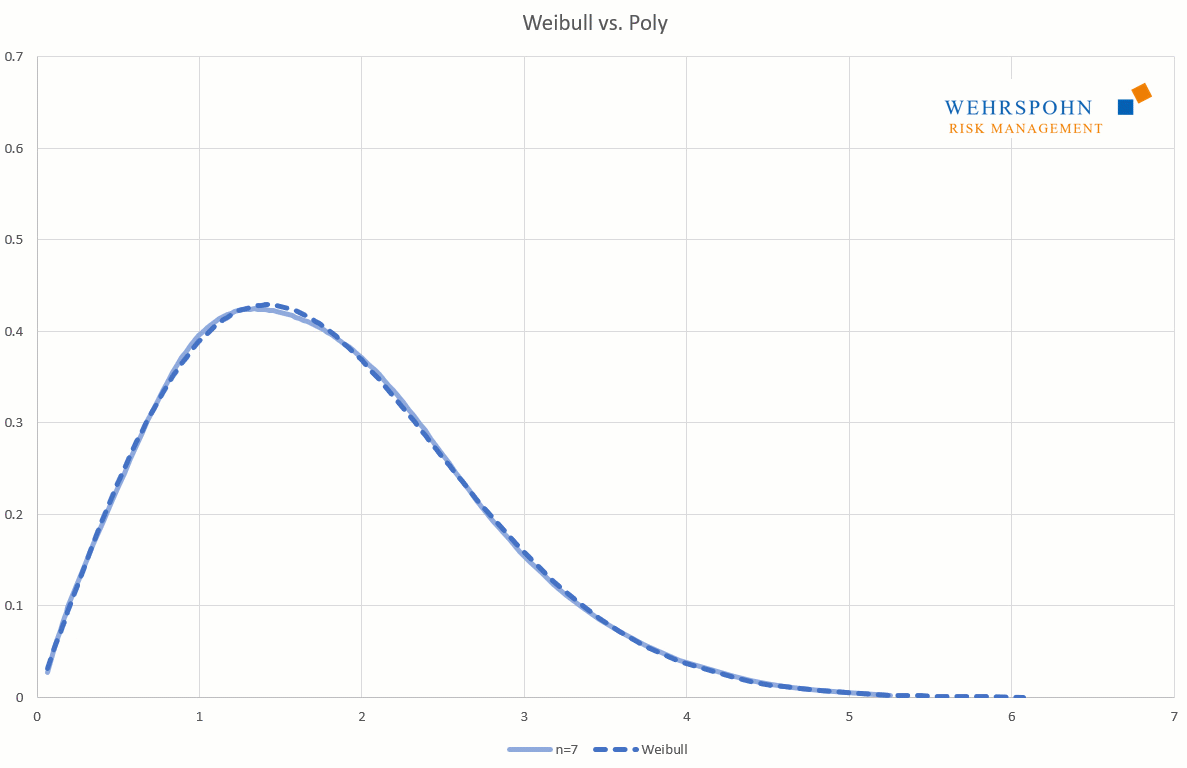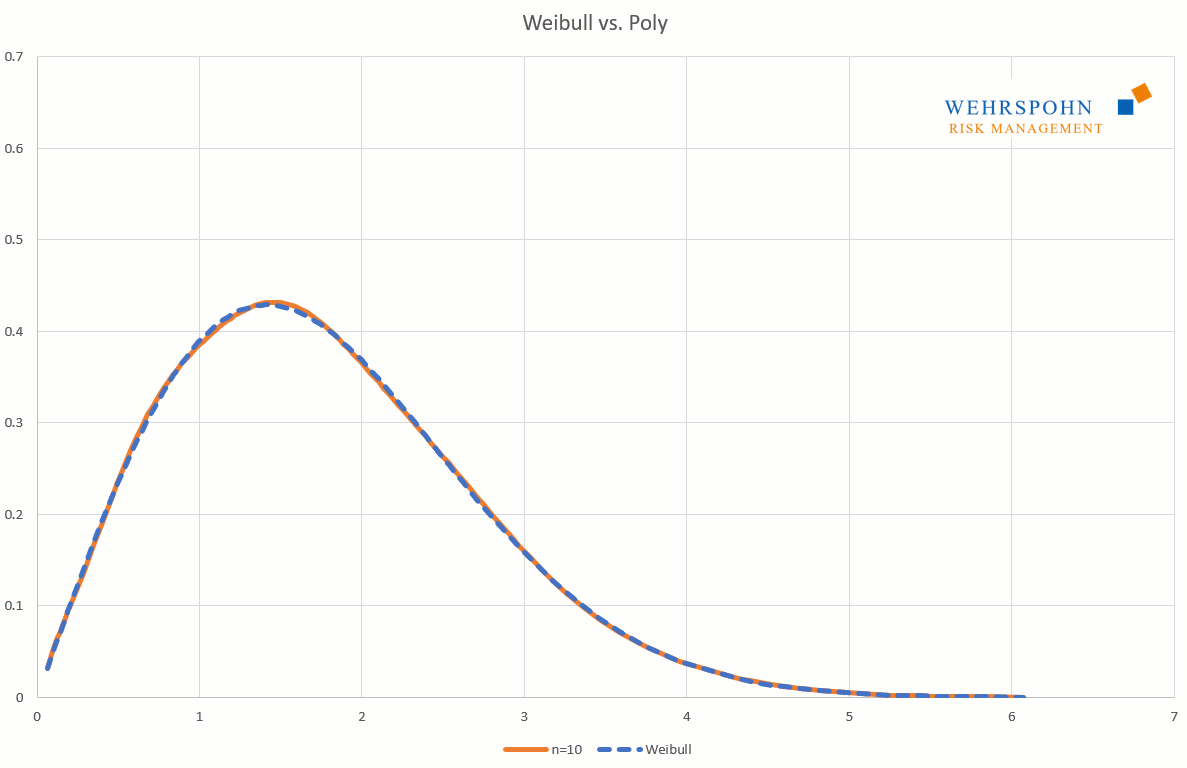
Poly distributions are a universal key. Due to their flexibility with a sufficiently high degree n of the polynomial, they can bring out special features in the data that other distributions cut off.

They can also adapt to many standard distributions so precisely that it is no longer possible to distinguish between them for practical purposes.

[1] They were introduced by Thomas Keelin under the name MetaLog distributions. Cf. Thomas W. Keelin (2016) The Metalog Distributions. Decision Analysis 13(4):243-277.

[2] The only prerequisite is that the underlying relationship is continuous in the first place and has finite moments. Expected value, variance etc. should therefore exist and there should be no jumps or spikes.

[3] The maximum order can be controlled to avoid possible overfitting.