Expert- und Poly-Verteilungen

Anwendungen im Risikomanagement müssen fallweise Experteneinschätzungen eines Sachverhalts und Datenauswertungen gleichermaßen gerecht werden können.

Standardverteilungen sind jedoch in der Regel auf eine feste Form mit geringen Variationsmöglichkeiten eingeschränkt. Diese Restriktionen aufzuweichen und flexiblere und anpassungsfähigere Instrumente zur Verfügung zu haben ist seit langem ein Ziel der Risikoverantwortlichen.

Im Enterprise Risk Evaluator, in Risk Kit und unseren weiteren Systemen gibt es daher ein Spektrum von Verteilungen mit vielfältigen Formen und Eigenschaften. Neu hinzugekommen sind jetzt die Expert- und Poly-Verteilungen. Sie können an den Rändern begrenzt oder offen sein, erweitern die Freiheiten von Experten und passen sich den Besondernheiten in den Daten an.

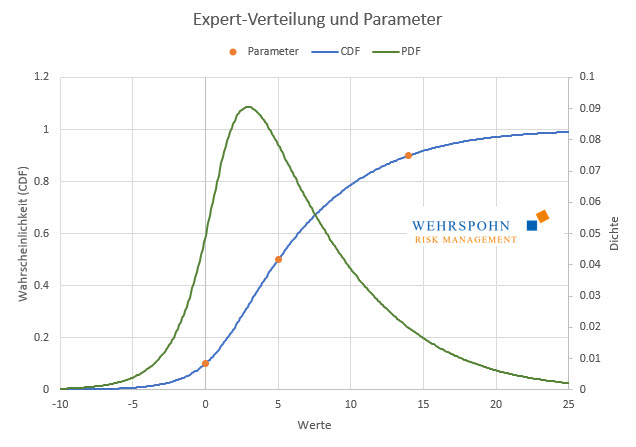
Die Expert-Verteilung ist ein Spezialfall der Poly-Verteilungen. Sie legt ihre Form über drei Quantile und ggf. Minimum und Maximum fest, falls die Verteilung beschränkt sein soll. Sie knüpft damit gedanklich an Dreiecks- und PERT-Verteilung an, ist aber in ihrem Verlauf gestaltungsfähiger. Sie ermöglicht etwa auch eine einseitig oder beidseitig unbegrenzte Darstellung von Auswirkungen. Sie kann damit in Bereichen eingesetzt werden, in denen man einen maximalen Schaden nicht ohne weiteres angeben kann.

Die Quantile, mit denen die Expert-Verteilung bestimmt wird, sind symmetrisch um den Median, es sind also das p-Quantil, der Median selbst und das 1-p-Quantil. Zusätzlich können ggf. untere und / oder obere Grenzen für den Wertebereich angegeben werden.

Die Verteilung geht exakt durch die angegebenen Punkte.

Poly-Verteilungen sind ein neues[1] und sehr flexibles Werkzeug bei der Beschreibung von Risiken. Sie gewinnen ihre Anpassungsfähigkeit durch ihren Aufbau als Polynom. Ähnlich wie sich eine Taylor-Reihe hinreichend hohen Grades an stetige und glatte Funktionen beliebig genau annähern kann, passen sich Poly-Verteilungen sehr detailliert an Daten oder Experteneinschätzungen an.[2]

Poly-Verteilungen können an den Grenzen alle Formen annehmen. Sie können beidseitig unbegrenzt sein (Poly), links- oder rechtsseitig begrenzt (PolyL bzw. PolyR) oder beidseitig begrenzt (PolyLR).

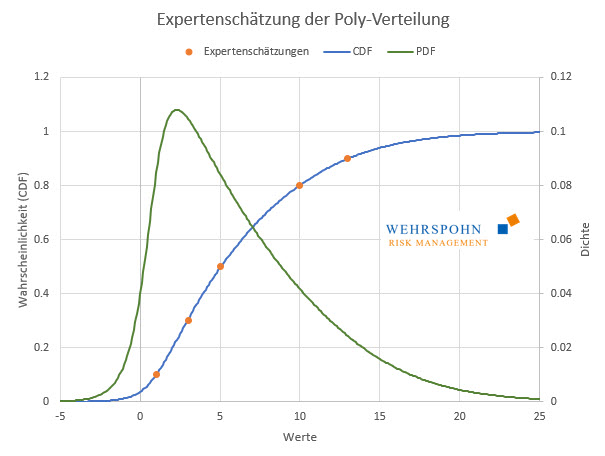
Die Koeffizienten der Polynome sind abstrakt und für Experten nicht zugänglich. Werden die Verteilungen über Experteneinschätzungen parametrisiert, erfolgt dies daher über eine Liste von Quantilen also Paaren von Werten und Wahrscheinlichkeiten in der Funktion CalibratePoly, die aus den Quantilen die Polynom-Koeffizienten ermittelt.

Anders als bei der Expert-Verteilung, einem Spezialfall der Poly-Verteilung, müssen die Quantile nicht symmetrisch um den Median sein, sondern können frei gewählt werden. Die Liste muss mindestens drei und kann beliebig viele Punkte enthalten. Zusätzlich können bei Bedarf untere und obere Grenzen vorgegeben werden. Die Verteilung wird so ausgewählt, dass sie möglichst nahtlos auf die Angaben passt. Grenzen werden dabei immer exakt getroffen.[3]

Die zweite wichtige Anwendung der Poly-Verteilungen ist ihre Anpassung an Daten. Bei beobachteten Daten ist das eine Selbstverständlichkeit. Aber auch simulierte Daten spielen eine wichtige Rolle.

Im ERM sollen alle wesentlichen Risiken des Unternehmens in einer Analyse gemeinsam betrachtet werden. Bei vielen Unternehmen gibt es jedoch spezielle Risikoarten, die so wichtig sind, dass sie gesonderte Aufmerksamkeit erhalten und auf diese Risikoart spezialisierte Systeme eingesetzt werden, die selbst Simulationen durchführen. Typische Beispiele sind Treasury-Anwendungen oder der Rohstoffeinkauf.

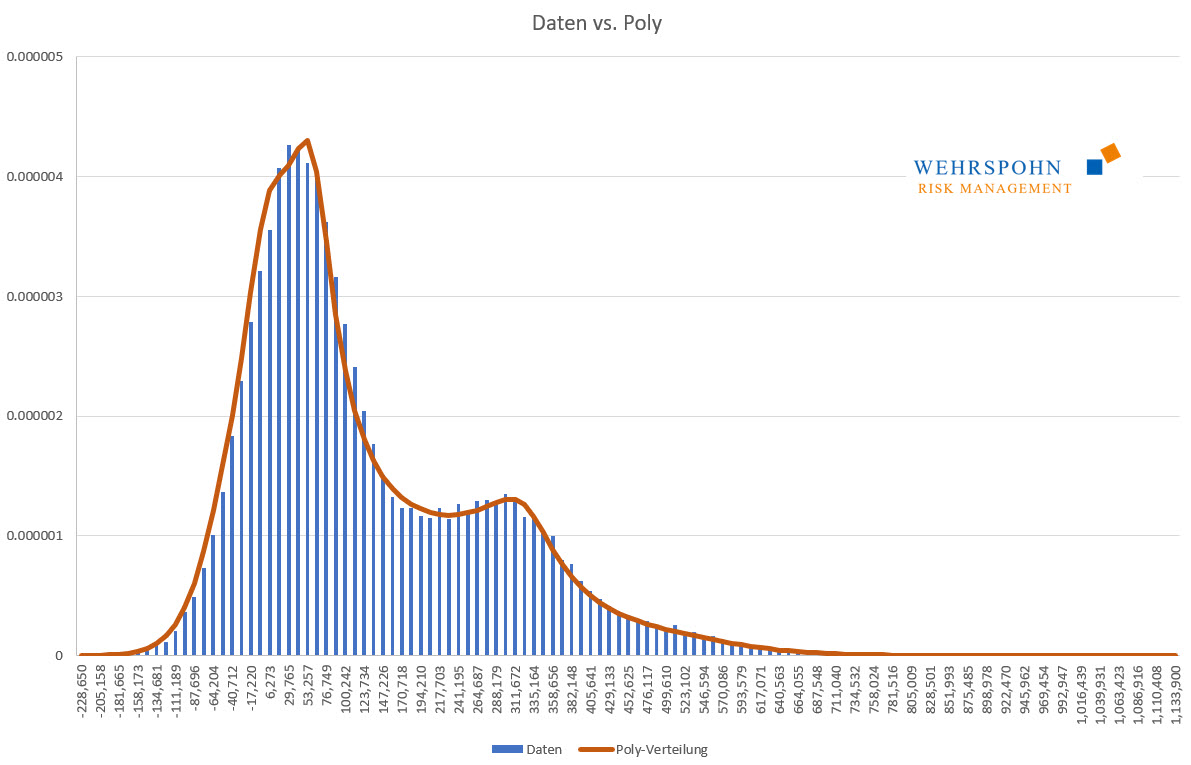
Mit Poly-Verteilungen können die Ergebnisse spezialisierter Simulationen sehr exakt mit sehr geringem Aufwand ins ERM übertragen werden. Dies ist auch dann der Fall, wenn die simulierten Verteilungen eine Form haben, die mit Standardverteilung nicht abbildbar ist, z.B. wenn sie mehrere Modi haben. In simulierten Verteilungen ergeben sich mehrere Modi auf natürliche Weise, wenn Großrisiken oder Krisen in der Simulation eintreten.

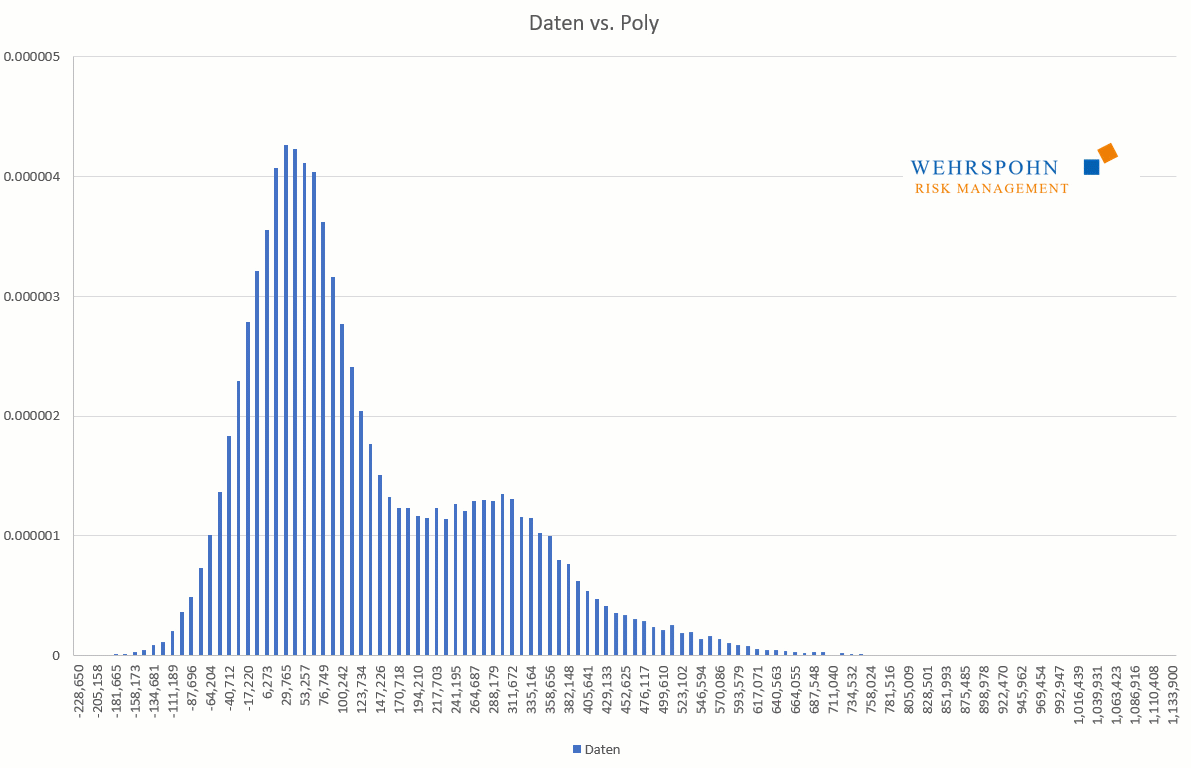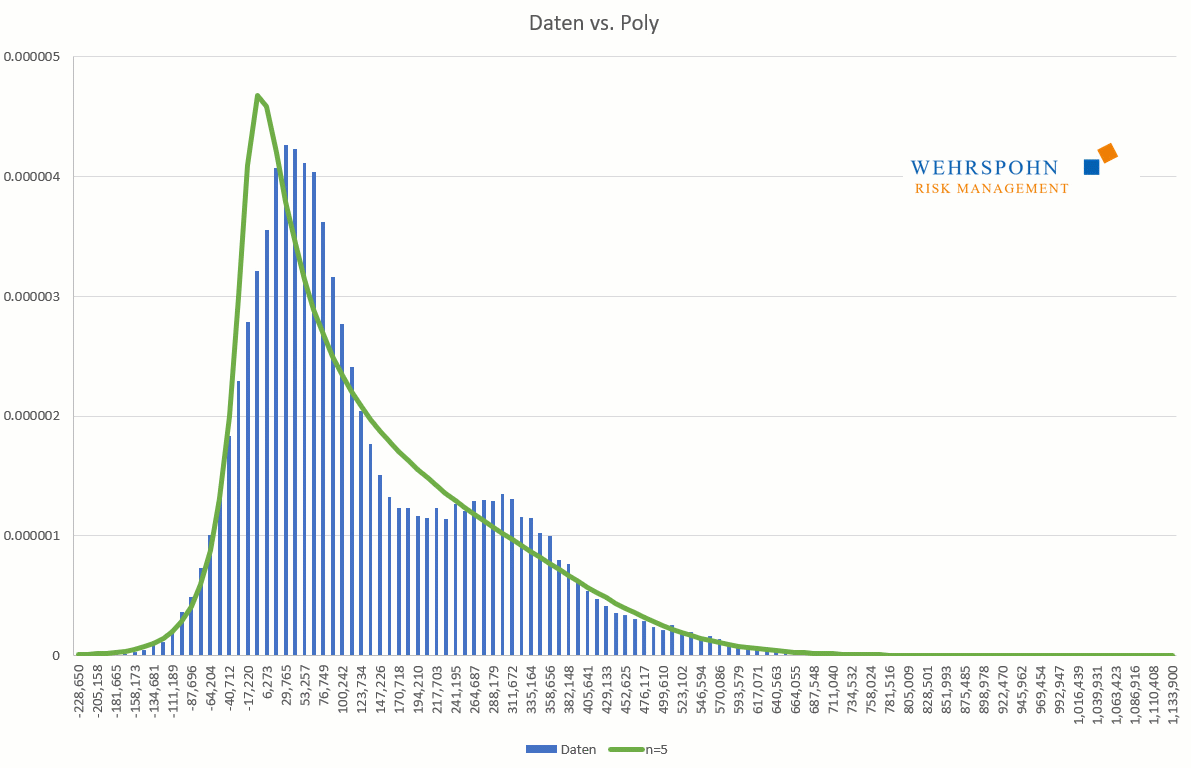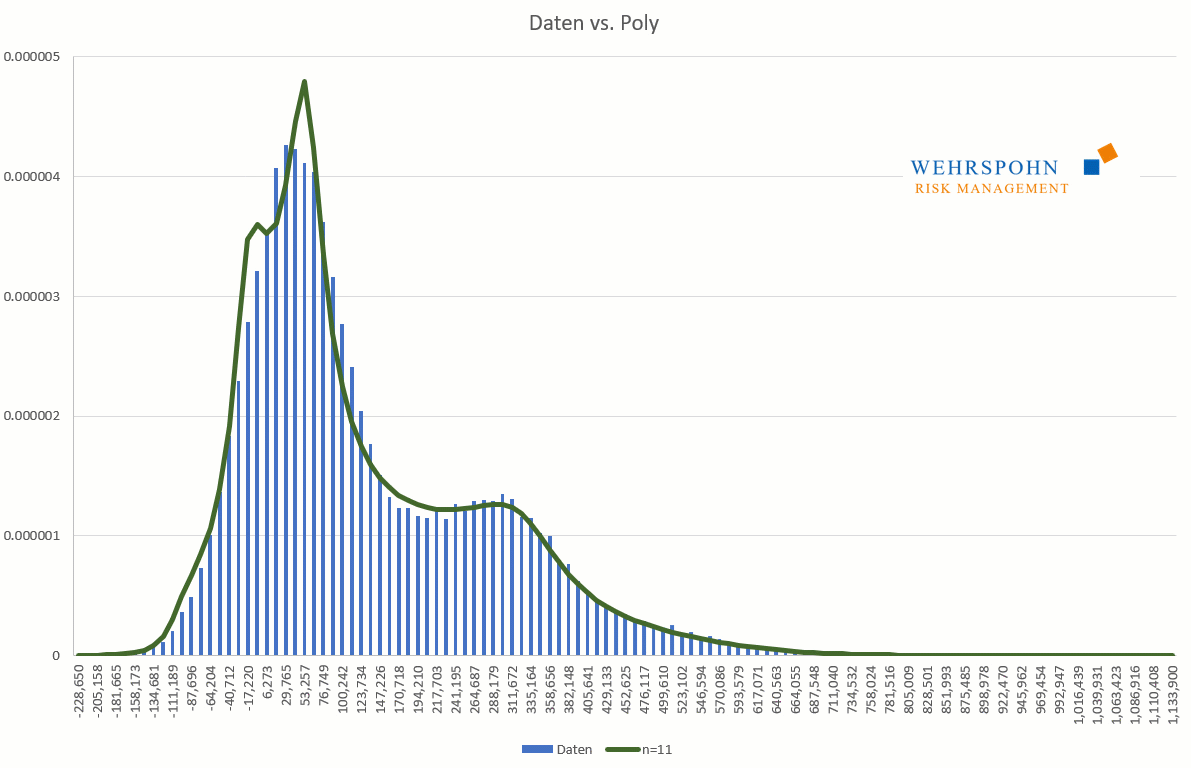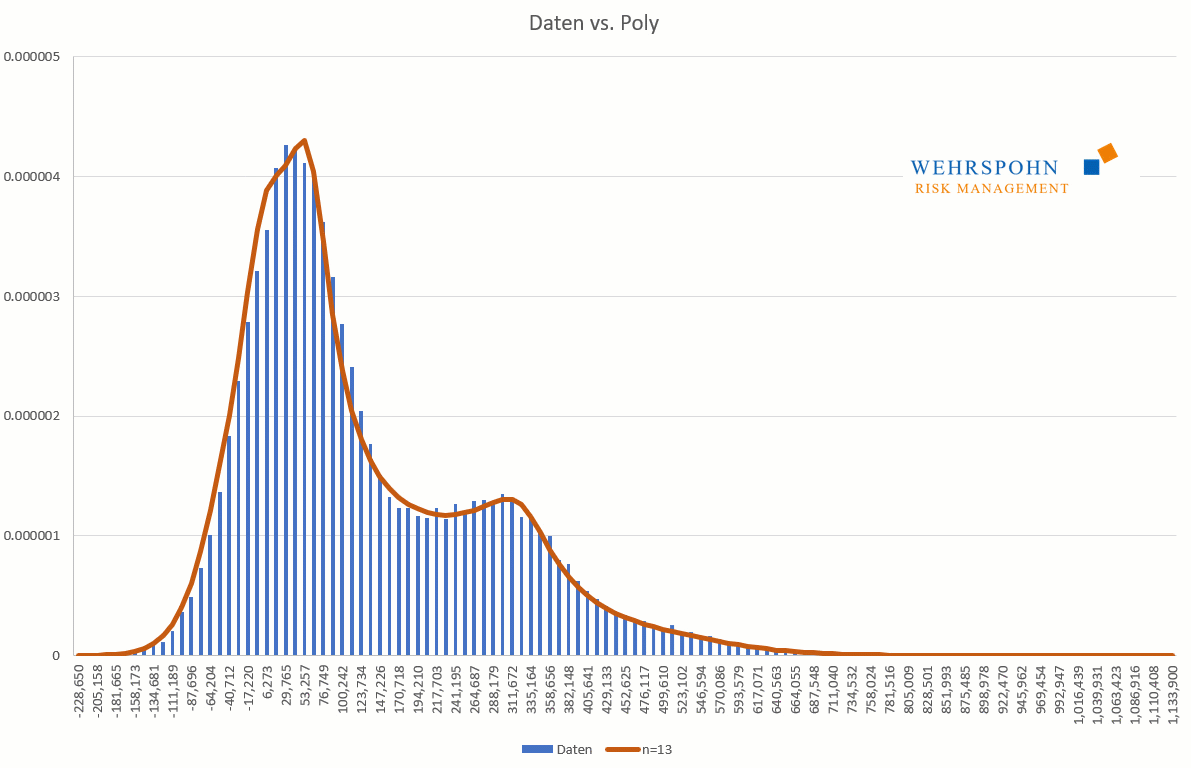
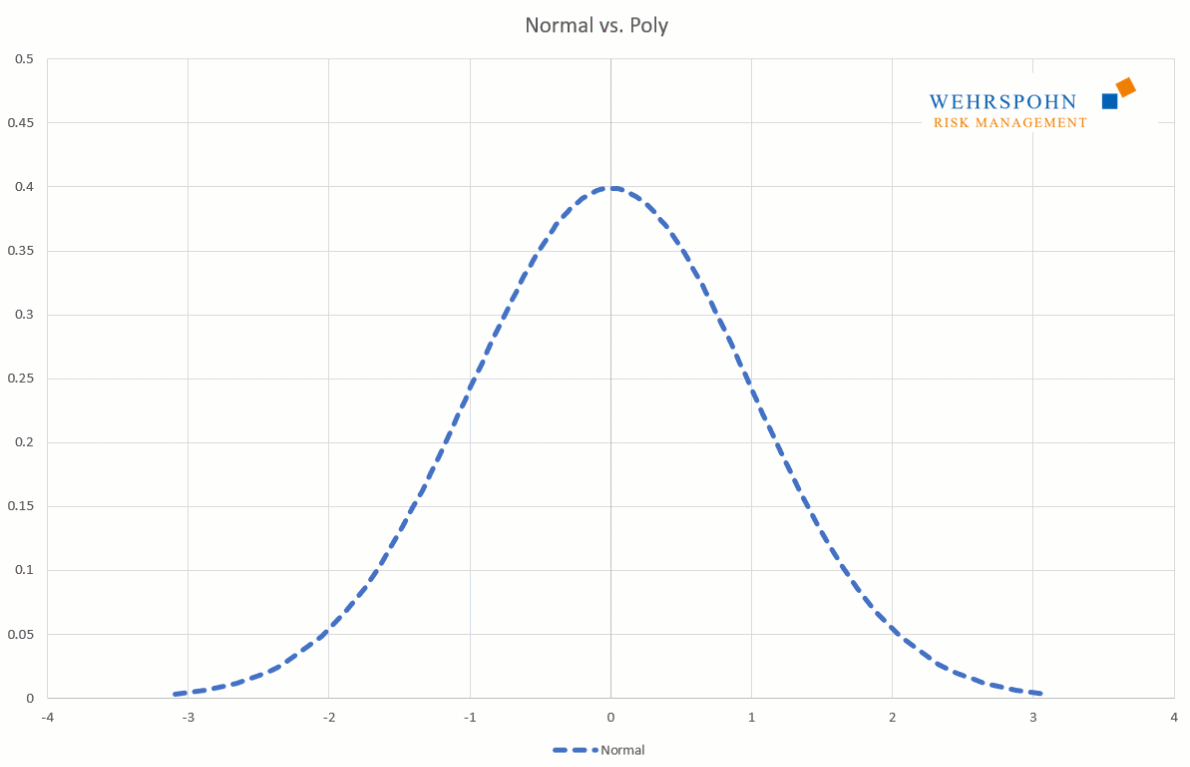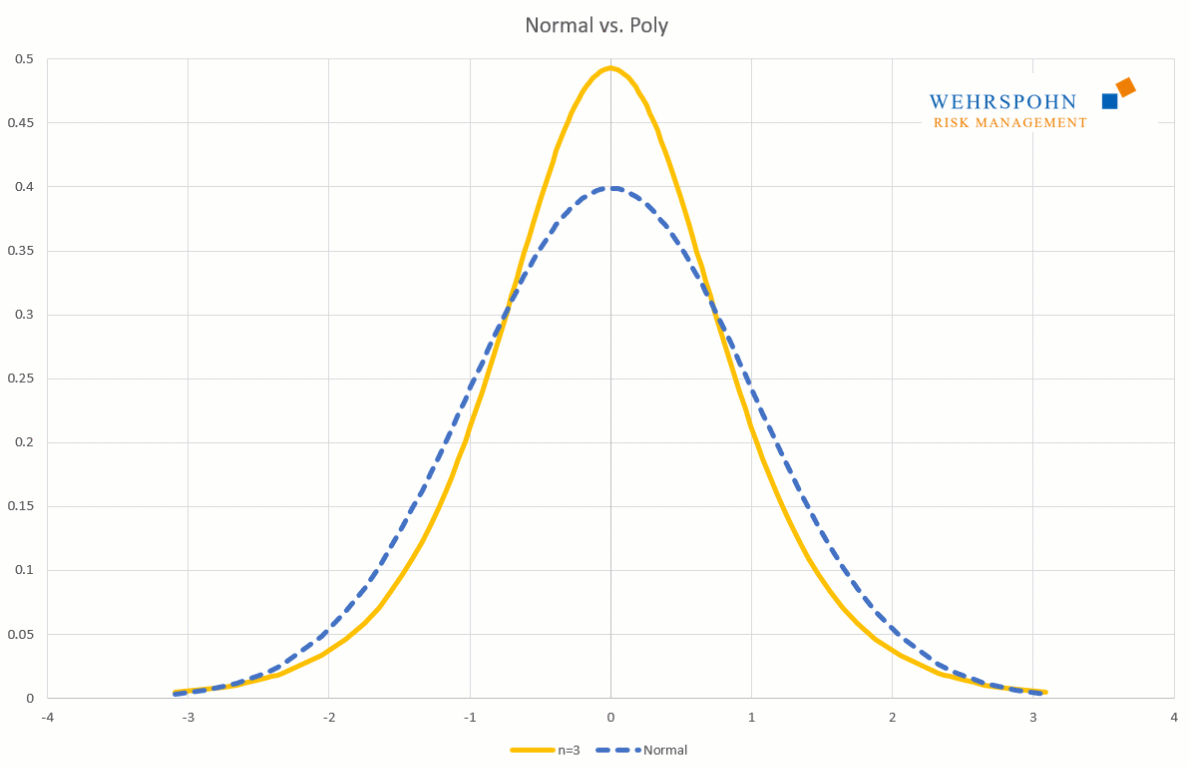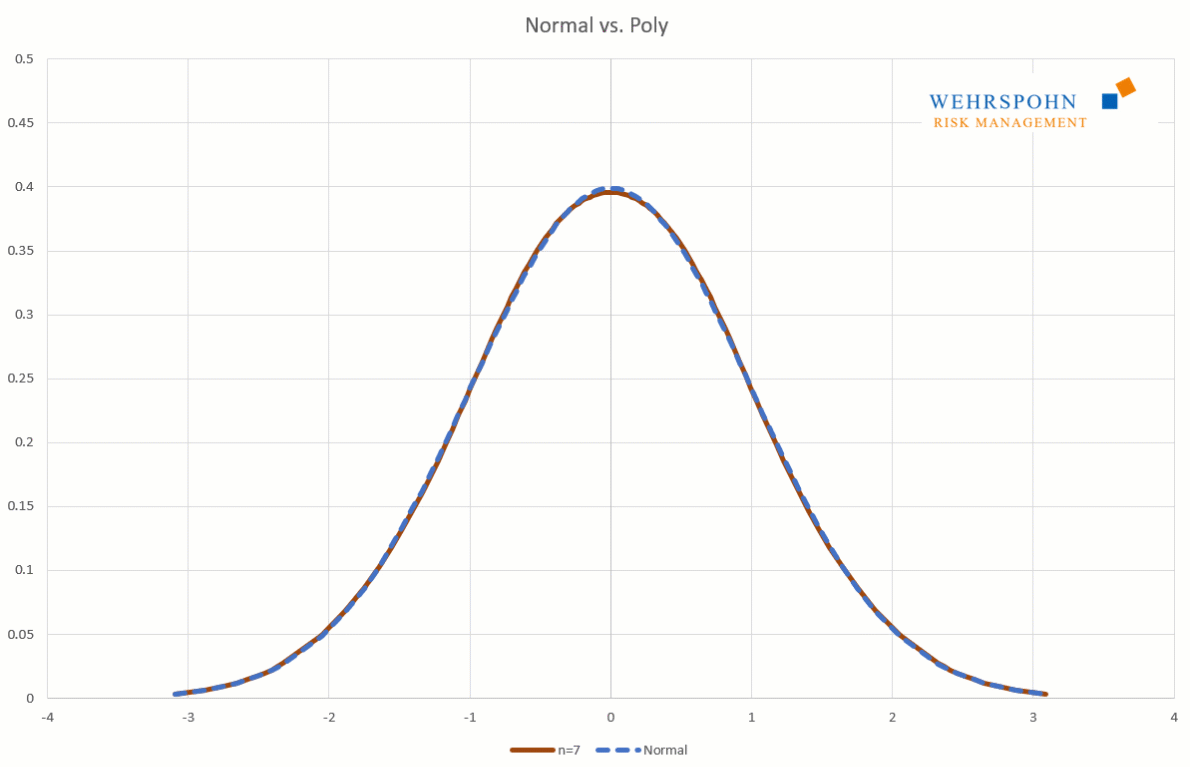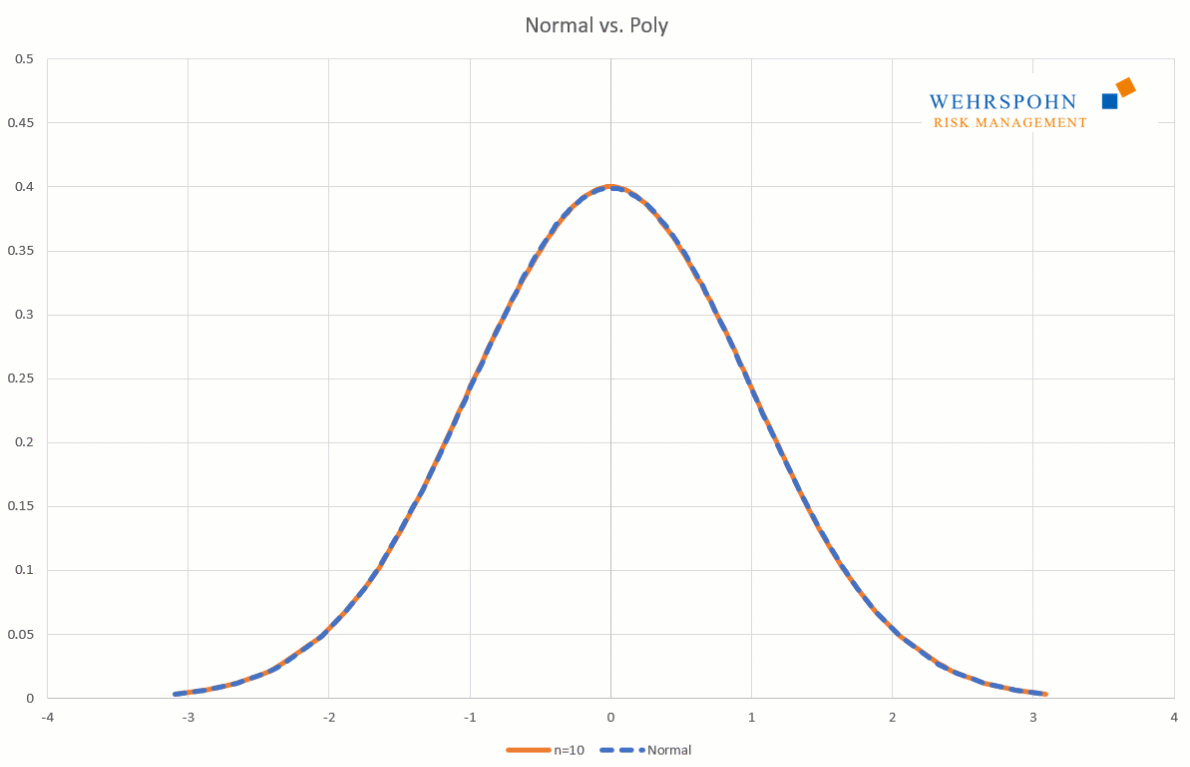
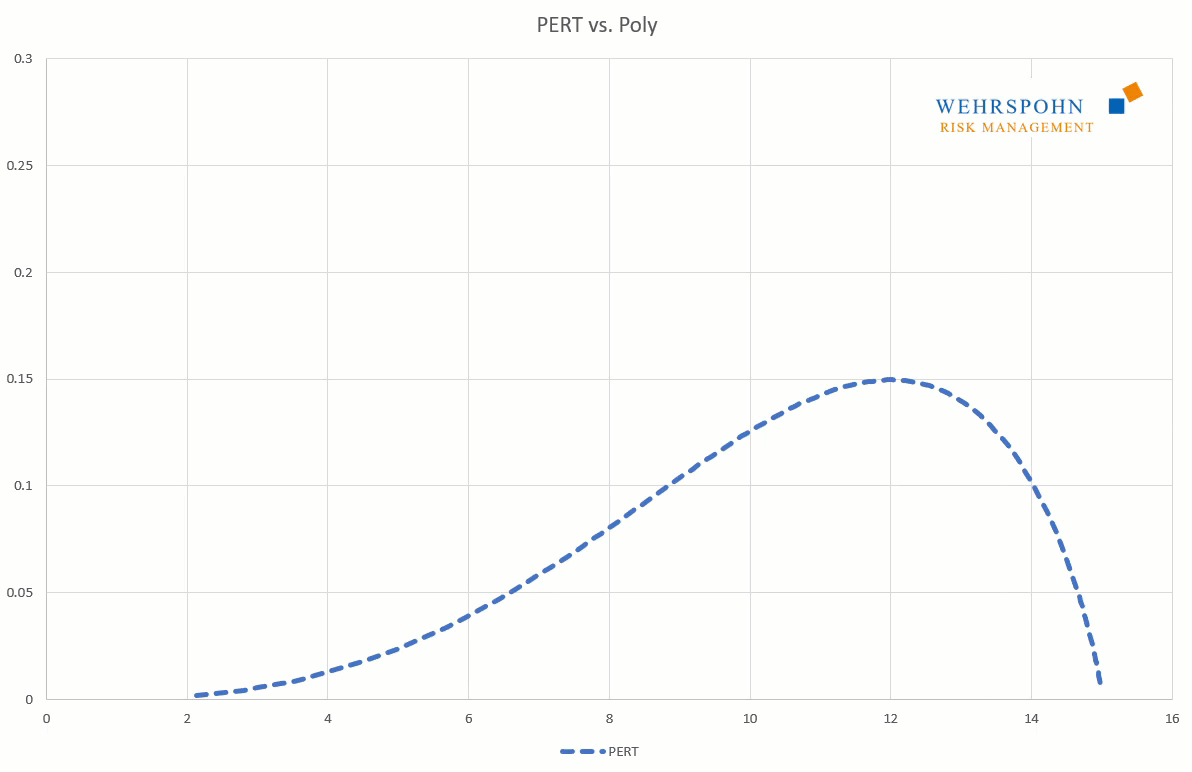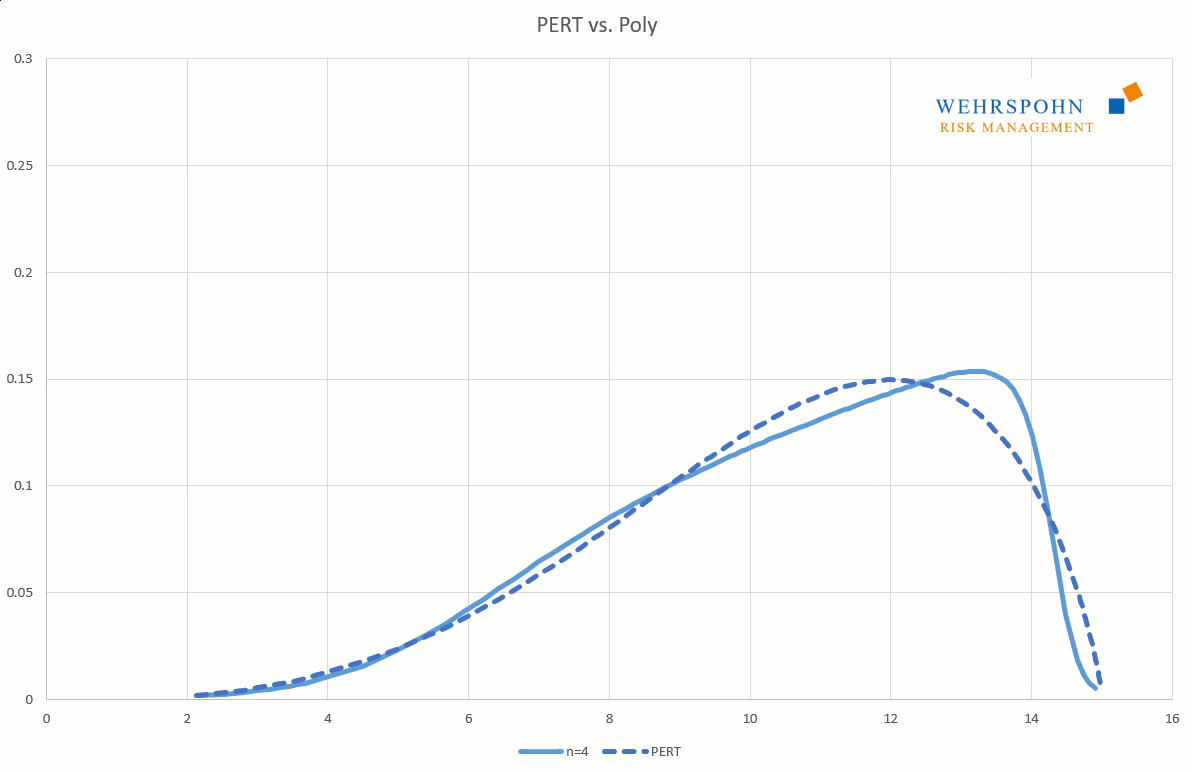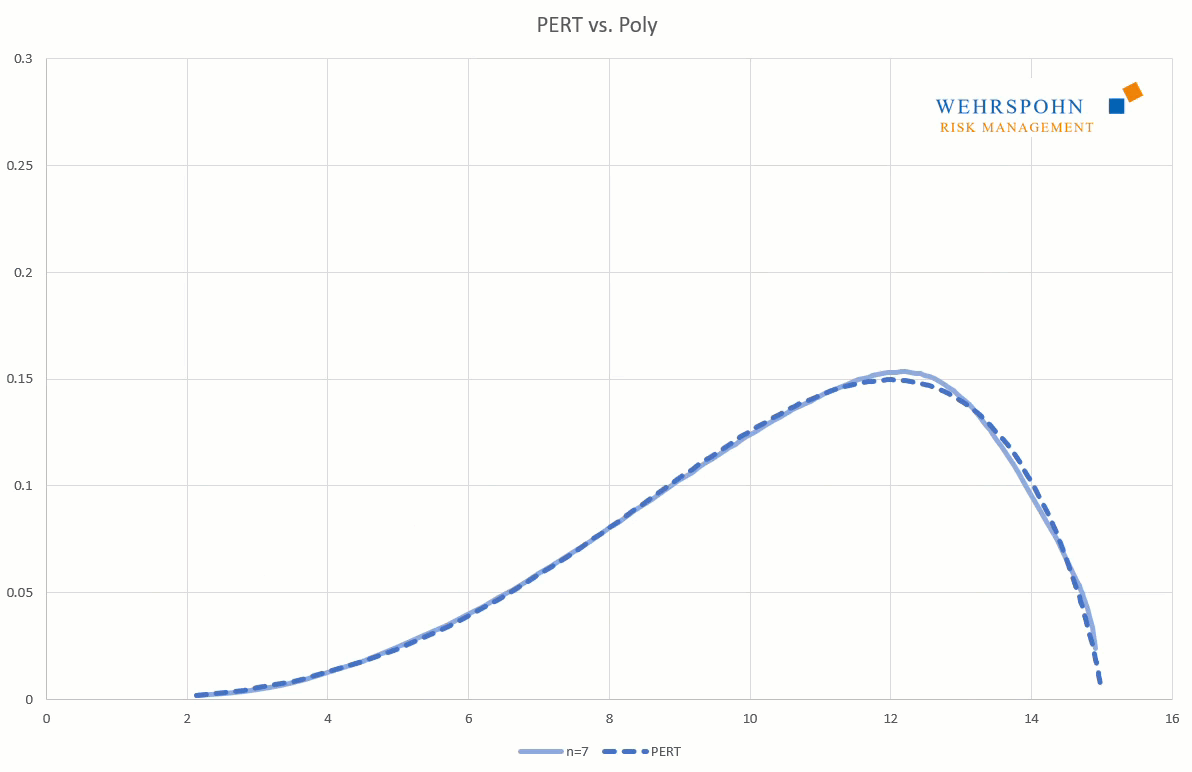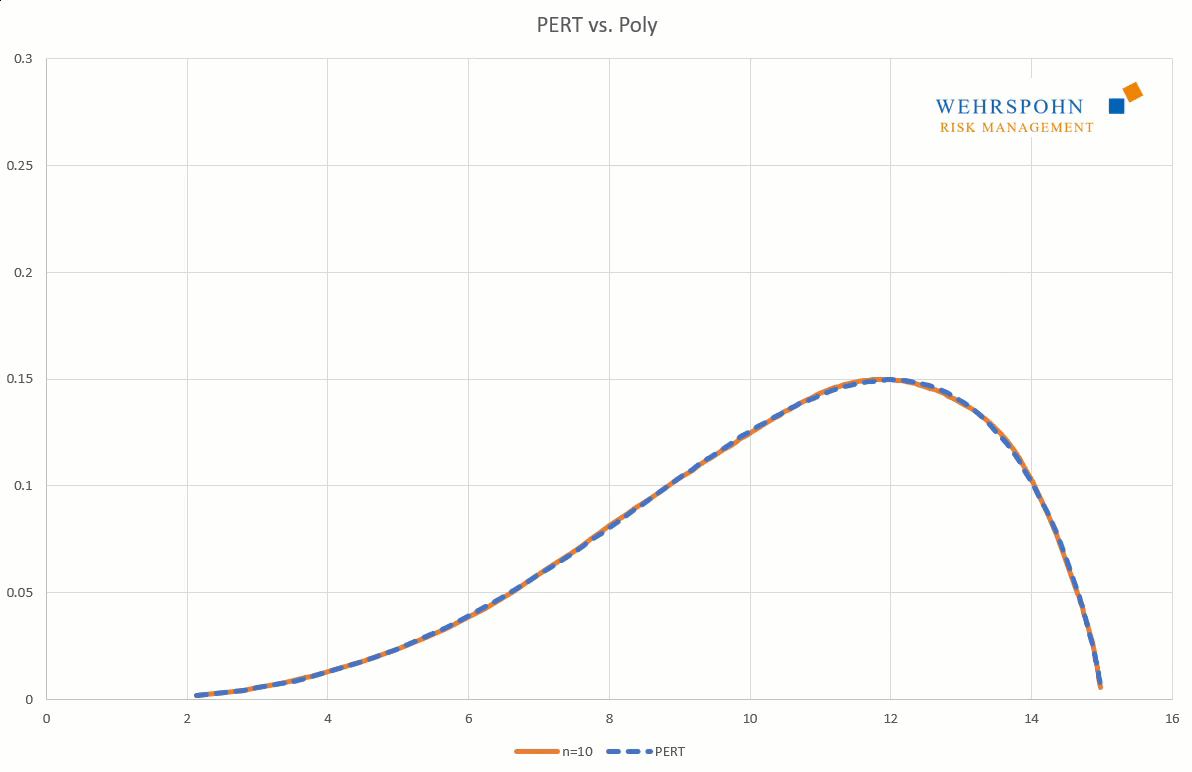
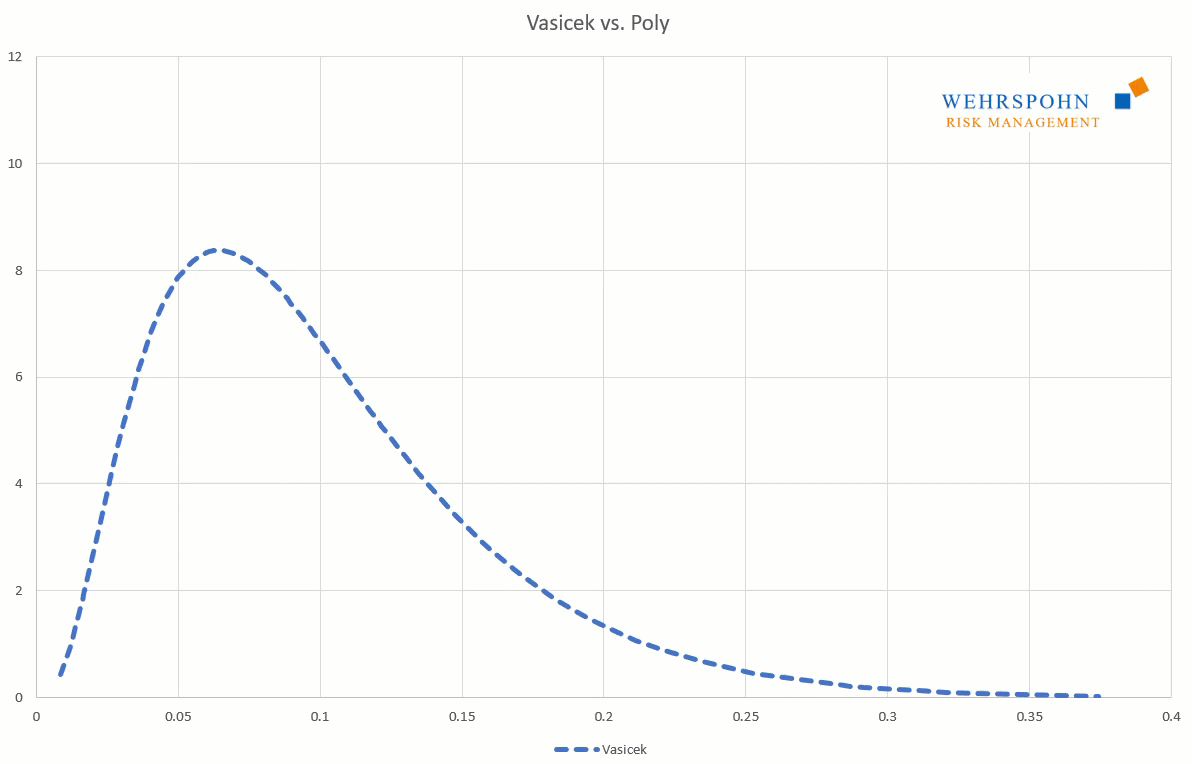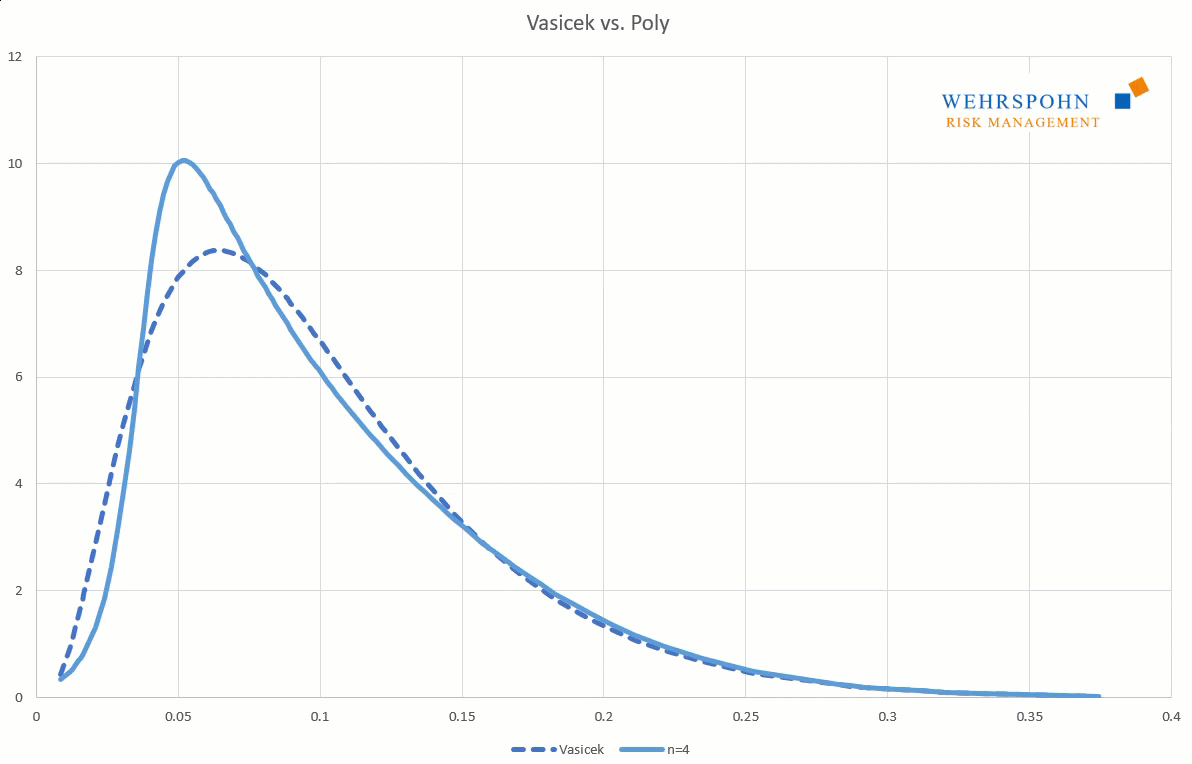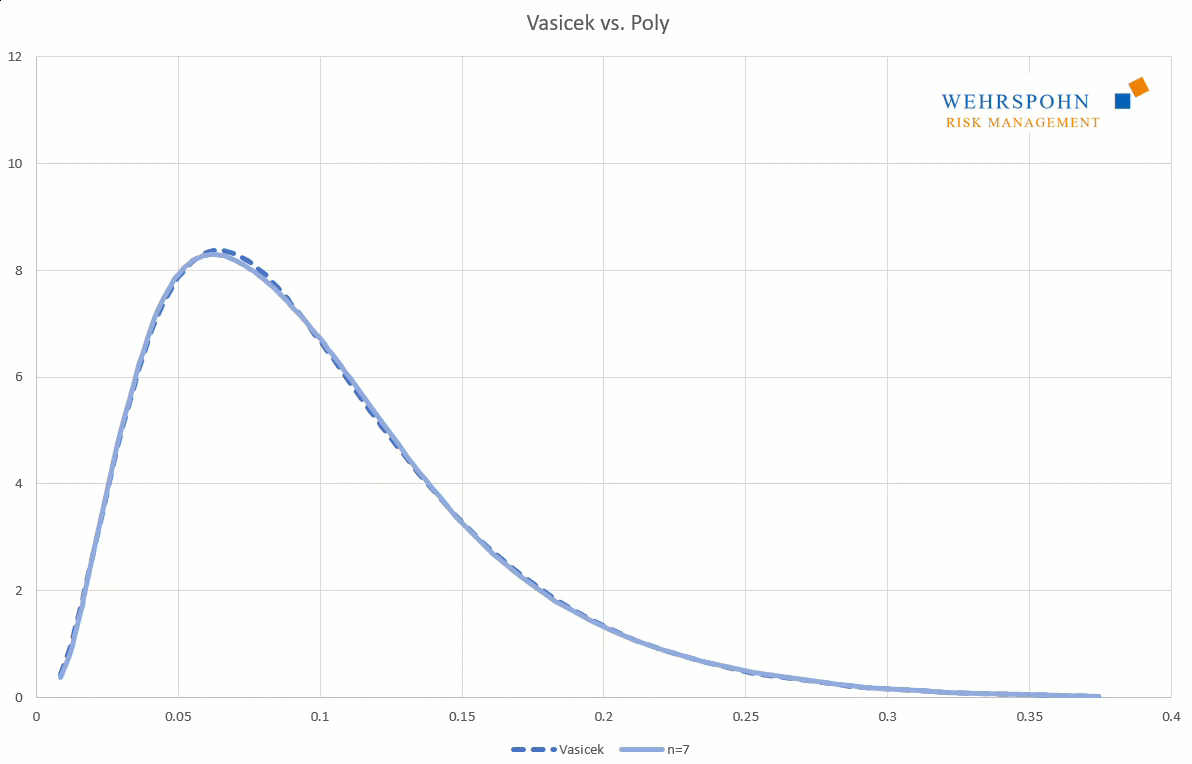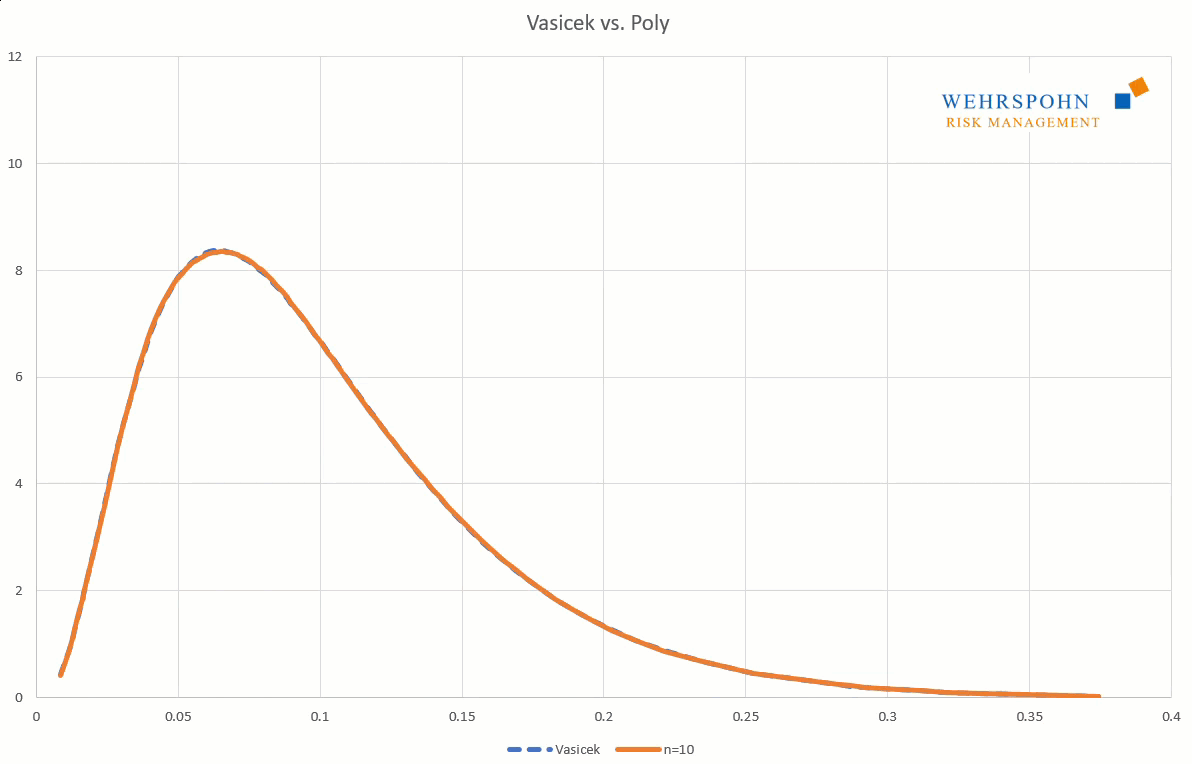
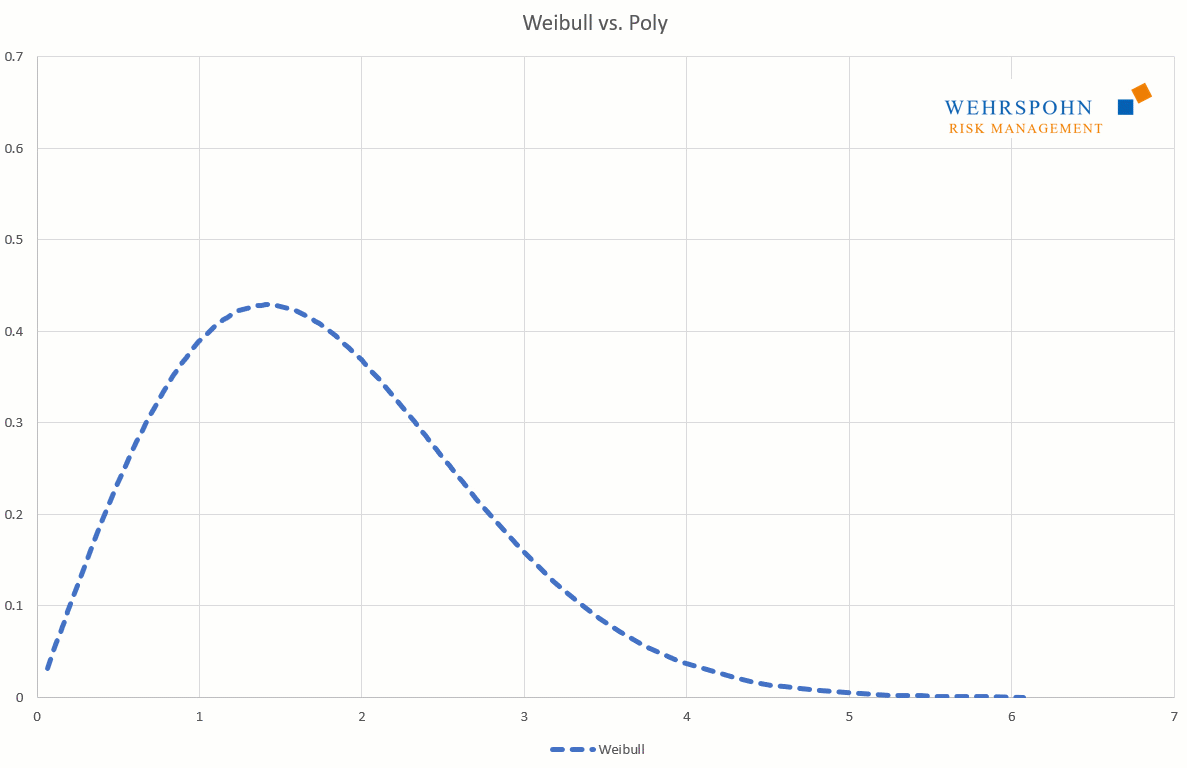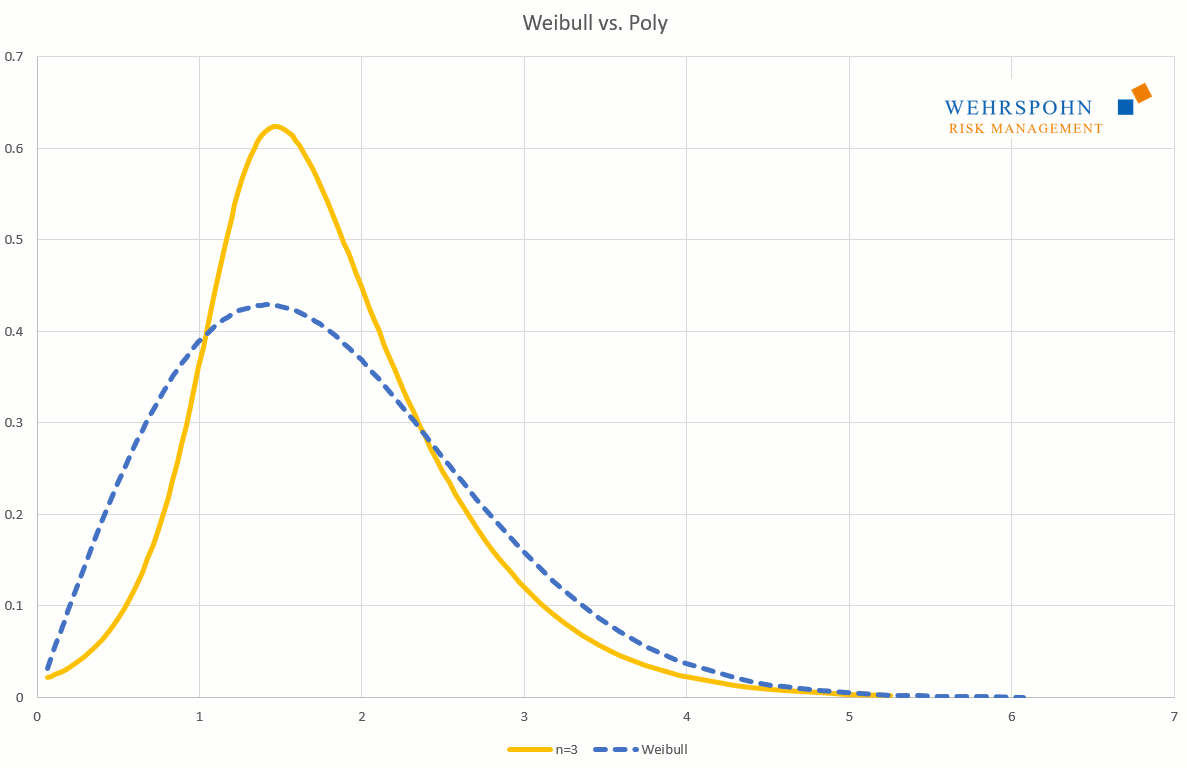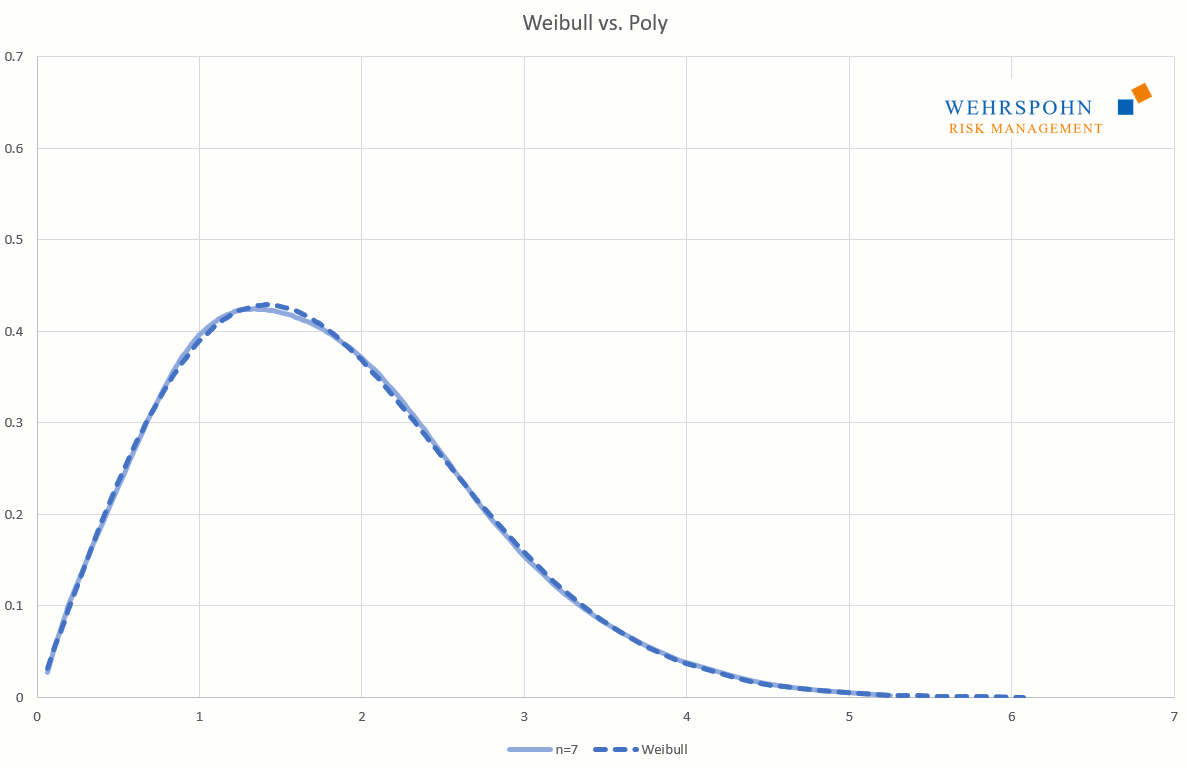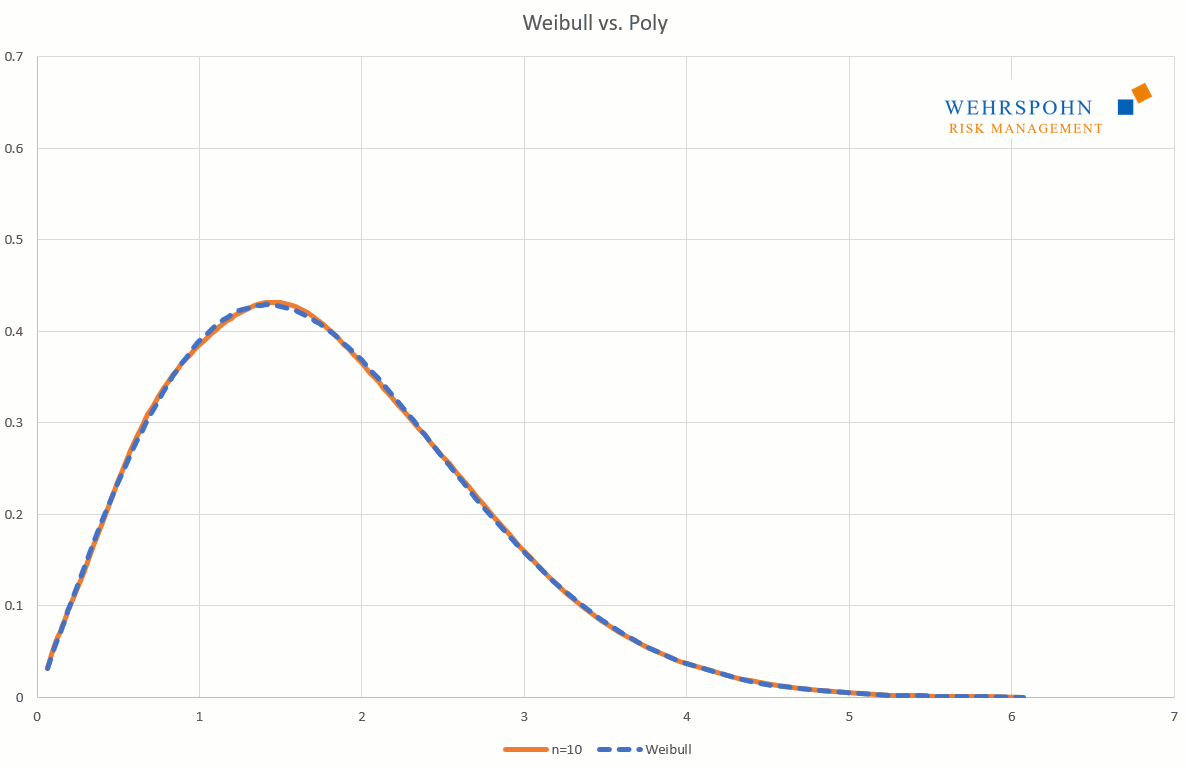
Poly-Verteilungen sind ein Universalschlüssel. Durch ihre Flexibilität bei ausreichend hohem Grad n des Polynoms können sie Besonderheiten in den Daten zur Geltung bringen, die andere Verteilungen abschneiden.

Sie können sich zudem an viele Standardverteilungen so genau anpassen, dass man sie für praktische Zwecke nicht mehr unterscheiden kann.

[1] Sie wurden von Thomas Keelin unter dem Namen MetaLog-Verteilungen eingeführt. Vgl. Thomas W. Keelin (2016) The Metalog Distributions. Decision Analysis 13(4):243-277.

[2] Voraussetzung ist lediglich, dass der zugrunde liegende Zusammenhang überhaupt stetig ist und endliche Momente hat. Erwartungswert, Varianz usw. sollten also existieren und es sollte keine Sprünge oder Spikes geben.

[3] Die maximale Ordnung kann dabei kontrolliert werden, um eventuelles Overfitting zu vermeiden.