Sensitivitäten: Probleme finden und Prioritäten setzen

Risikomanagement muss effizient sein und ist gezwungen mit knappen Ressourcen wirkungsvolle Entscheidungen zu treffen. Die problematischen Risikotreiber zu finden und begründete Prioritäten für das Management setzen zu können ist daher ein wichtiges strategisches Ziel einer Risikoanalyse.

Risk Kit und der Enterprise Risk Evaluator stellen Methoden zur Verfügung, um die Sensitivitäten - also die Wirkung von Risikofaktoren auf das Ergebnis - zu bewerten. Sie beantworten eine Vielzahl an möglichen Leitfragen:

• Welche Risikofaktoren wirken sich am stärksten auf das Ergebnis aus? Welches sind meine Top-Risiken?
• Wie groß ist die absolute Wirkung eines Risikofaktors auf das Ergebnis in der Einheit des Ergebnisses? 
• Wir wirken sich Risikoereignisse auf das Ergebnis aus, wenn sie eintreten?
• Kann ich erkennen, ob eine risikomindernde Maßnahme wirkungslos oder wirkungsschwach ist?
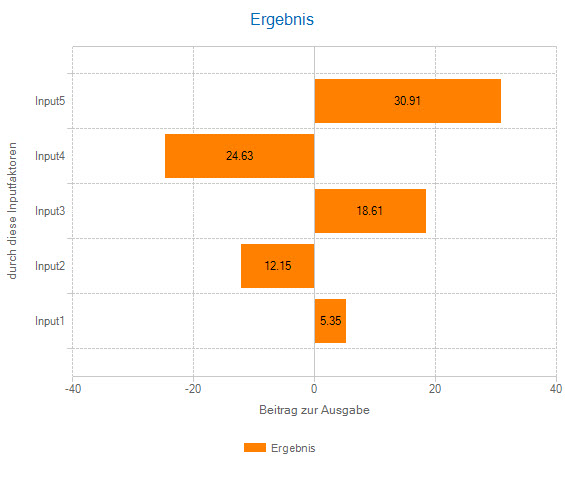
• Wie verteilen sich die Beiträge zum Gesamtrisiko auf die einzelnen Risikofaktoren?
• Wie kann ich die Ergebnisse tabellarisch und als Grafik kommunizieren?

Hier eine Übersicht.

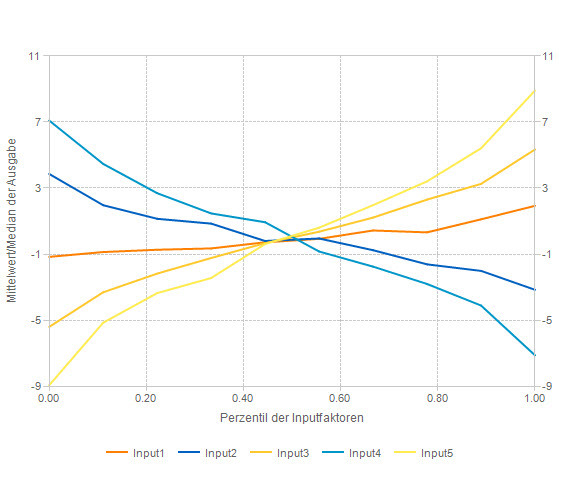
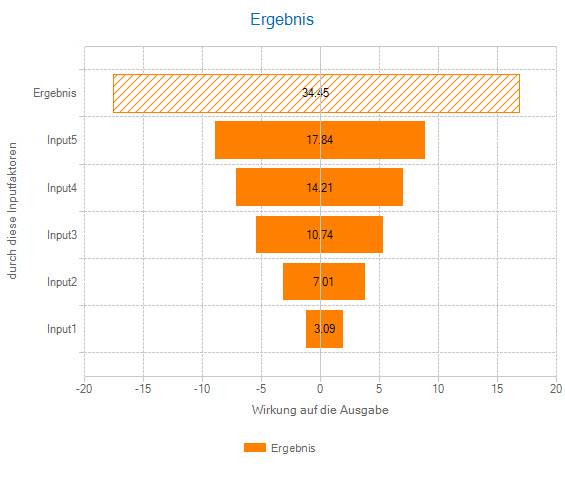
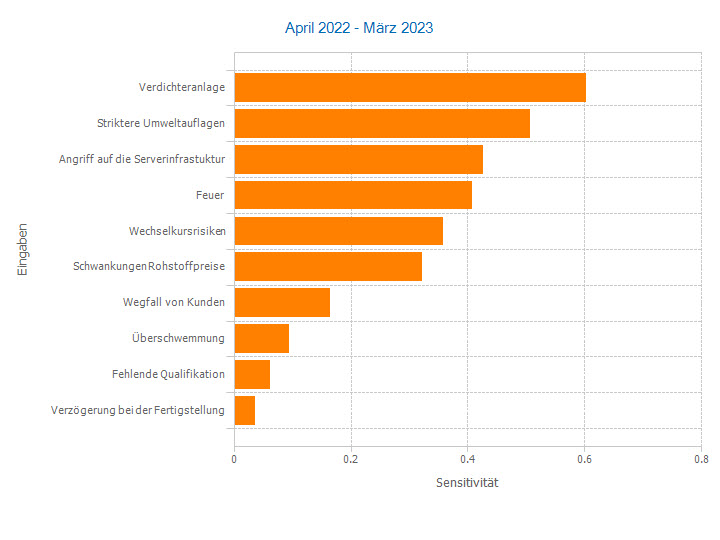
Absolute Sensitivitäten erfassen die Wirkung eines Risikofaktors auf das Ergebnis in der Einheit des Ergebnisses. Alle Risikofaktoren haben damit eine einheitliche 'Währung' und sind untereinander vergleichbar. Sie werden berechnet, indem für einen Quantilbereich des Risikofaktors (z.B. 0-10%, 10-20% usw.) der Mittelwert oder der Median des Ergebnisses berechnet wird.

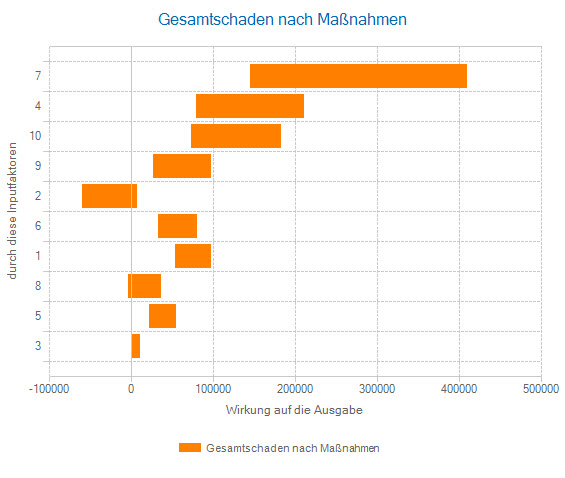
Das Spider Chart und das Tornado Diagramm veranschaulichen diese Schritte. Sie sind ein erprobtes Mittel der Risikokommunikation.

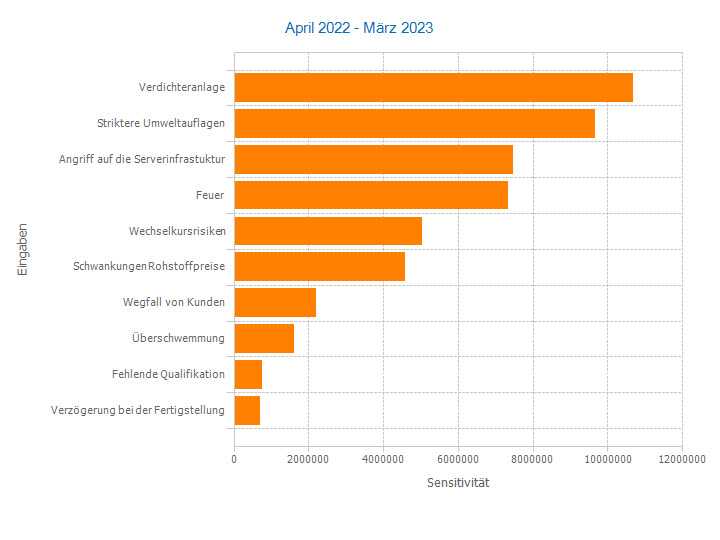
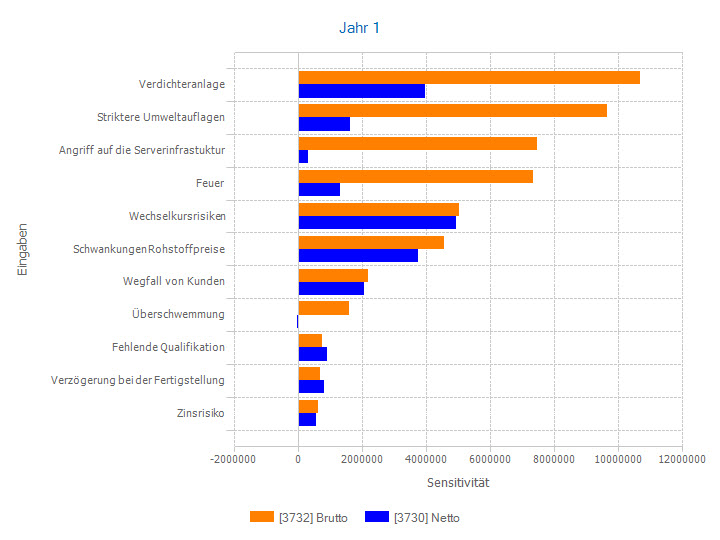
Im Enterprise Risk Management ist dieser Sensi-Typ besonders interessant, denn wenn ein Risiko nicht durch Maßnahmen gemindert wird, ändert sich seine Wirkung auf das Ergebnis in vielen Fällen nicht. Die Sensitivität dieses nicht gemanagten Risikos bleibt dann ebenfalls stabil. Dies ist eine wichtige Voraussetzung dafür Maßnahmen, die die Auswirkungen des Risikofaktors auf das Ergebnis nicht reduzieren, identifizieren zu können.

Für ereignisgesteuerte Risikofaktoren, die nicht immer eintreten, sondern nur manchmal, oder die nur wenige Werte annehmen, gibt es bedingte absolute Sensitivitäten als speziellen Sensi-Typ. Hier werden alle Ergebnisse, für die der Risikofaktor denselben Wert hat, durch ihren Mittelwert oder Median auf eine Zahl verdichtet. Nur auf den unterschiedlichen Werten des Risikofaktors werden dann die absoluten Sensitivitäten berechnet.

Vorteil der bedingten absoluten Sensitivitäten ist, dass der Fall, dass das Risiko gar nicht eingetreten ist oder einen festen Wert hat und dementsprechend auch keine unterschiedliche Wirkung entfaltet, aus der Analyse herausgenommen wird. Im Focus steht dann die Frage, 'in welchem Bereich ändert sich das Ergebnis, wenn sich der Risikofaktor ändert?' Faktoren, die durchaus Unsicherheit ins System bringen, aber auch oder sogar in erster Linie Chancen sind und keine Risiken, werden so sichtbar.

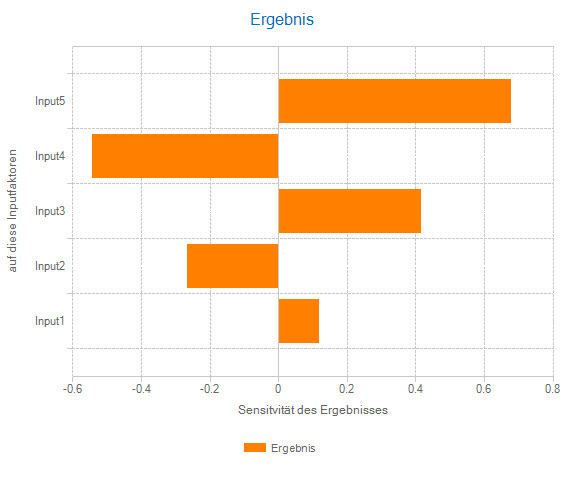
Relative Sensitivitätskonzepte setzen Größen zueinander ins Verhältnis. Sie haben daher in der Regel keine Einheit und bewegen sich in einem gewissen Wertebereich.

Wichtige relative Sensitivitäten sind lineare Korrelationen, Rangkorrelationen, Beiträge zur Varianz (quadrierte Rangkorrelationen, deren Summe auf 1 standardisiert ist) und Betafaktoren. Ihr Betrag weißt aus, wie eng Risikofaktor und Ergebnis zusammenhängen. Ihr Vorzeichen gibt die Richtung des Zusammenhanges an.

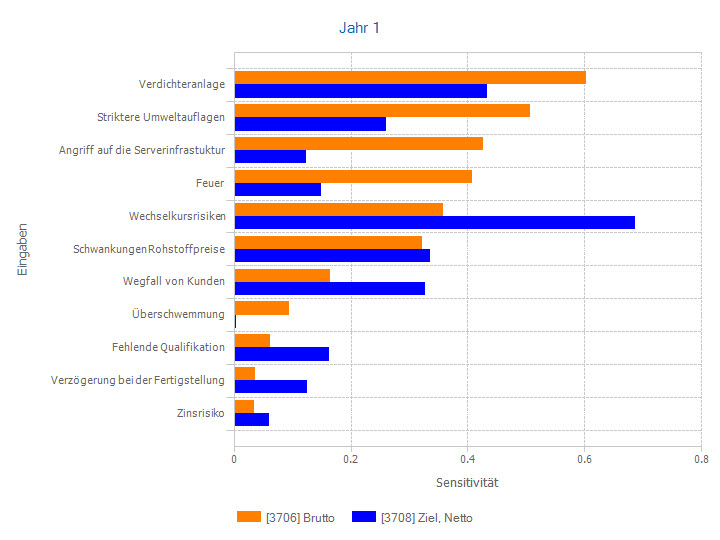
Wenn Maßnahmen ergriffen werden, ergibt sich daraus die Besonderheit, dass sich auch relative Sensitivitäten von Risikofaktoren ändern, für die es keine Maßnahmen gibt. Sie werden in der Regel größer, da sozusagen ihr Beitrag zu einem nach Maßnahmen kleineren Kuchen jetzt relativ gesehen größer wird.

Korrelationen nehmen Werte zwischen -1 und 1 an. Beiträge zur Varianz können nicht negativ werden. Ihre Werte liegen zwischen 0 und 1.

Betafaktoren sind in ihrem Wertebereich nicht begrenzt, liegen aber meist zwischen -3 und 3. Ist ihr Betrag größer als 1, bedeutet dies, dass die Kovarianz zwischen Faktor und Ergebnis betragsmäßig größer ist als die Varianz des Ergebnisses.

Wenn der Risikofaktor sehr stark streut, ist Vorsicht geboten, denn es kann dadurch ein zufälliger Scheinzusammenhang festgestellt werden. Die Verwendung des Betafaktors bietet sich dadurch vor allem dann an, wenn es einen bekannten strukturellen Zusammenhang zwischen einem Risikofaktor und dem Ergebnis gibt, also z.B. zwischen einem Aktienkurs und einem Aktienindex, in dem die Aktie selbst enthalten ist.

Risiken verursachen Kosten - auch durch das Risikomanagement selbst. Hinzu kommen Kapitalkosten für die Risikokapitalunterlegung, die in der Risikotragfähigkeit von IDW PS 340 seit kurzem gefordert wird. Die Kosten auf die Risiken zurückzuverteilen, ist also eine natürliche Anwendung des Verursacherprinzips.

Um die Risikobeiträge zu ermitteln, geben Sie zusätzlich das Risikomaß an, das auf die Risiken zurückverteilt werden soll. Dies kann ein Value at Risk (Quantil) sein ebenso wie ein Expected Shortfall. Die absoluten Sensitivitäten oder Betafaktoren erhalten das Vorzeichen des linearen Zusammenhanges zwischen Risikofaktor und Ergebnis und werden so skaliert, dass sie in der Summe dieses Risikomaß ergeben.